Les suites et séries/Les suites arithmético-géométriques

Tout cours sur les suites aborde rapidement les fameuses suites arithmétiques, géométriques et arithmético-géométriques. Il faut dire que ces suites sont assez utilisées dans de nombreux domaines et il est important de les connaitre par cœur. Elles sont de plus assez simples à comprendre, ce qui fait que nous allons les étudier maintenant.

Les suites arithmétiques

Les suites arithmétiques sont des suites où les termes augmentent d'un pas régulier : on compte de 2 en 2, de 3 en 3, de 1.6 en 1.6, de 39 en 39, etc.

Exemple de suite arithmétique de raison 4.

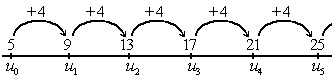
Dit autrement, la différence entre un terme et le suivant est une constante et chaque terme s’obtient en additionnant une constante au terme précédent. En clair, on a :

$u_{n+1}=u_{n}+k$

La constante $k$, le pas de la suite, est appelée la raison de la suite La raison d'une suite arithmétique peut être aussi bien positive que négative, et même nulle ! Et le signe de la raison influence la croissance ou décroissance de la suite.

• Si la raison est nulle, chaque terme est égal au précédent : la suite est constante.
• Si la raison est positive, les termes de la suite ne cessent d'augmenter avec le rang : la suite est croissante.
• Si la raison est négative, les termes diminuent progressivement quand le rang augmente : la suite est décroissante.

Les suites arithmétiques sont donc soit croissantes, soit décroissantes : ce sont donc des suites monotones.

L'équation précédente peut aussi se réécrire comme suit :

$u_{n}=u_{0}+n\times k$

Les suites géométriques

Les suites géométriques sont assez similaires aux suites arithmétiques, la seule différence étant que l'addition est remplacée par une multiplication : chaque terme est un multiple du précédent

Suite géométrique

Une suite de ce type est définie par la fonction de récurrence suivante :

$u_{n+1}=u_{n}\times k$

La constante $k$ est encore une fois appelée la raison de la suite et elle peut être aussi bien positive que négative.

L'équation précédente peut se réecrire comme suit :

$u_{n}=u_{0}\times k^{n}$

Contrairement aux suites arithmétiques, les suites géométriques ne sont pas forcément monotones. Et cette fois-ci, la croissance ou décroissance de la suite ne dépend pas du signe de la raison, mais de sa valeur. Dans les grandes lignes, tout dépend si la raison est négative ou positive, et si sa valeur absolue est comprise entre 0 et 1. Une suite géométrique de raison positive sera une suite monotone, alors qu'une raison négative donnera une suite alternée (le signe des terme s'inverse d'un terme à l'autre).

• Si la raison est positive, la suite est obligatoirement monotone.
  • Si la raison est supérieure à 1, chaque terme sera plus grand que le précédent et la suite est croissante.
  • Si la raison est de 1, chaque terme est égal au précédent : la suite est constante.
  • Si la raison est plus petite que 1 mais malgré tout positive, chaque terme sera plus petit que le précédent, mais reste positif : la suite est décroissante.
• Si la raison est négative, chaque terme positif est suivi d'un négatif et réciproquement : la suite est alors dite alternée.

Les suites arithmético-géométriques

Les suites arithmético-géométriques sont des généralisations des suites géométriques et arithmétiques : elles sont en quelque sorte les deux à la fois. Chaque terme se calcule en multipliant le précédent, avant d'ajouter une autre constante. La constante par laquelle on multiplie le terme précédent est appelé la raison de la suite, alors que l'autre constante additionnée est appelée la constante additive.

$u_{n+1}=a\times u_{n}+b$

On peut signaler qu'une suite arithmétique est une suite arithmético-géométrique de raison multiplicative 1, alors qu'une suite géométrique est une suite arithmético-géométrique où la constante additive nulle.

Obtenir l'expression paramétrée de la suite est possible, bien que compliqué. Pour cela, nous allons déterminer la différence entre la suite arithmético-géométrique voulue et une suite géométrique de même raison et de premier terme identique. Nous allons voir ce que cela donne sur un exemple, avant de généraliser.

Rang	Suite géométrique	Suite arithmético-géométrique	Différence entre les deux suites
1	$u_{0}$	$u_{0}$	0
2	$u_{0}\times a$	$u_{0}\times a+b$	$b$
3	$u_{0}\times a^{2}$	$u_{0}\times a^{2}+ab+b$	$ab+b$
4	$u_{0}\times a^{3}$	$u_{0}\times a^{3}+a^{2}b+ab+a$	$a^{2}b+ab+a$
5	$u_{0}\times a^{4}$	$u_{0}\times a^{4}+a^{3}b+a^{2}b+ab+a$	$a^{3}b+a^{2}b+ab+a$
...	...	...	...
n	$u_{0}\times a^{n}$	$u_{0}\times a^{n}+b(a^{n}+a^{n-1}+...+a^{2}+a^{1}+a^{0})$	$b(a^{n}+a^{n-1}+...+a^{2}+a^{1}+a^{0})$
...	...	...	...

On verra dans le chapitre sur les sommes partielles, que $(a^{n}+a^{n-1}+...+a^{2}+a^{1}+a^{0})={\frac {a^{n+1}-1}{a-1}}$. En faisant le remplacement, on a :

$u_{n}=u_{0}\times b^{n}+b\left({\frac {a^{n+1}-1}{a-1}}\right)$

On obtient avec pas mal de manipulations algébriques :

$u_{n}=a^{n}\left(u_{0}-{\frac {b}{1-a}}\right)+{\frac {b}{1-a}}$

Il est possible de démontrer cette relation autrement, bien que la démonstration soit moins intuitive. En voici une démonstration juste en-dessous.

Démonstration

Pour faire cette démonstration, nous allons tenter de nous ramener d'une suite arithmético-géométrique à une simple suite géométrique, que l'on sait traiter. Pour cela, nous allons étudier la suite définie par : $u_{n}=v_{n}+t$ avec $t={\frac {b}{1-a}}$ On a alors : $u_{n+1}=au_{n}+b=a(v_{n}+t)+b$ Vu que $u_{n+1}=v_{n+1}+t$ : $v_{n+1}=a(v_{n}+t)+b-t=av_{n}+at+b-t=av_{n}$ La suite $v_{n}$ est donc une suite géométrique. On a donc : $u_{n}=v_{n}+t=a^{n}v_{0}+t=a^{n}(u_{0}-t)+t$ En remplaçant $t$ par sa valeur $t={\frac {b}{1-a}}$, on trouve : $u_{n}=a^{n}\left(u_{0}-{\frac {b}{1-a}}\right)+{\frac {b}{1-a}}$