Électricité/Les circuits linéaires et leurs lois

Électricité

La physique de l’électricité

• Les grandeurs électriques : intensité, tension, puissance
• Le passage du courant dans un solide : la résistance

Les circuits électriques

• Les dipôles : générateurs et récepteurs
• Les circuits électriques
• Les lois des circuits électriques

Le régime continu et les circuits résistifs/linéaires

• Les résistors
• Les générateurs : piles, batteries et autres
• Les associations de résistors
• Les circuits linéaires et leurs lois
• Les quadripôles linéaires

Le régime transitoire : bobines et condensateurs

• Le condensateur
• La bobine
• Bobines et condensateurs en série/parallèle
• Les circuits RL, RC, LC et RLC

Le régime alternatif

• Le continu et l'alternatif
• Le régime sinusoïdal
• L'impédance : l'équivalent sinusoïdal de la résistance
• Les quadripôles en régime sinusoïdal
• Le transformateur monophasé
• Les redresseurs

Annexes

• Notions de sécurité électrique

Les lois de Kirchhoff permettent de démontrer d'autres lois très utiles pour analyser les circuits électriques. Parmi celles-ci, nous allons surtout étudier les lois qui valent pour ce qu'on appelle les circuits linéaires, aussi appelés circuits résistifs. Pour simplifier, un circuit linéaire ne contient que des générateurs parfaits et des résistances. La définition plus formelle est qu'un circuit linéaire ne contient que des dipôles dits linéaires. Ceux-ci sont des composants pour lesquels la relation entre tension et intensité à leurs bornes est affine (et non pas linéaire). Pour le moment, les composants linéaires que nous connaissons se limitent aux résistances et aux générateurs parfaits combinés à des résistances (générateurs réels vus précédemment).

Le principe de superposition

Le principe de superposition est de loin le plus simple à comprendre et à appliquer. Celui-ci s'applique pour les circuits linéaires, qui comprennent plusieurs générateurs. On pourrait croire que leur étude est très compliquée, mais le théorème de superposition simplifie grandement les calculs.

Ce principe permet de calculer les tensions, courants et potentiels en un point avec une méthode très simple : il suffit de faire la somme des résultats obtenus en ne prenant en compte qu'un seul générateur. Pour un circuit avec N générateurs, on doit donc calculer N tensions différentes, avant d'en faire la somme. Chaque tension se calcul en ne gardant qu'un seul générateur, différent pour chaque tension. Les générateurs à ne pas prendre en compte sont simplement remplacés par un fil.

Un premier exemple d'application

Illustration du principe de superposition.

Prenons par exemple un circuit avec deux générateurs, comme le circuit à votre droite, noté (a). Celui-ci contient deux générateurs, reliés aux bornes de deux résistances en série. On connaît la tension aux bornes des générateurs, ainsi que les valeurs des deux résistances. On souhaite connaître le potentiel au milieu du circuit, entre les deux résistances, que nous noterons $P$. Le théorème de superposition nous dit de calculer le potentiel deux fois : une première fois en ne prenant en compte que le premier générateur, et la seconde en ne gardant que le second. Ces deux étapes sont illustrées par les deux circuits notés(b) et (c).

La première étape est illustrée par le circuit noté (b). Seul le second générateur est conservé, l'autre étant remplacé par un court-circuit. On peut alors calculer la tension P en appliquant un diviseur de tension.

$P_{2}=V_{2}\cdot {\frac {R_{1}}{R_{1}+R_{2}}}=-2,77V$

La seconde étape est illustrée par le circuit noté (c). Seul le premier générateur est conservé, l'autre étant remplacé par un court-circuit. On peut encore une fois calculer la tension P en appliquant un diviseur de tension.

$P_{1}=V_{1}\cdot {\frac {R_{2}}{R_{1}+R_{2}}}=8,88V$

On peut alors calculer la valeur du potentiel total en faisant la somme des deux potentiels précédents. On obtient :

$P=P_{2}+P_{1}=8,88V-2,77V=6,11V$

Un cas particulier : la loi de Pouillet

Quand un circuit ne contient qu'une seule maille, le principe de superposition permet de simplifier le circuit en réduisant drastiquement le nombre de générateurs et de résistances. Précisément, on peut fusionner tous les générateurs en un seul, dont la tension est la somme de celles des générateurs d'origine. Même chose pour les résistances, que l'on peut fusionner en une seule résistance, dont la valeur est la somme des résistances d'origine. Il s'agit d'une application des lois concernant les générateurs en série et les résistances en série. On peut alors utiliser ce résultat pour calculer le courant qui circule dans la maille, en divisant la tension fusionnée par la résistance équivalente.

Le théorème de Millman

Le théorème de Millman est une reformulation de la loi des nœuds, écrite avec des potentiels et des résistances. Prenons un nœud sur lequel convergent/divergent plusieurs branches. La loi des nœuds dit que la somme des courants de chaque branche reliée au nœud est nulle :

$0=I_{0}+I_{1}+I_{2}+\cdot \cdot \cdot +I_{n}$

Supposons que dans chaque branche numéro $i$, on trouve une résistance $R_{i}$. Il doit y avoir une tension $U_{i}$ aux bornes de la branche. D'après la loi d'Ohm, on a :

$0={\frac {U_{0}}{R_{0}}}+{\frac {U_{1}}{R_{1}}}+{\frac {U_{2}}{R_{2}}}+\cdot \cdot \cdot +{\frac {U_{n}}{R_{n}}}$

Chaque tension est la différence entre le potentiel au niveau du nœud $V_{M}$ et les potentiels aux autres extrémités des branches $V_{i}$. On a donc :

$0={\frac {V_{0}-V_{M}}{R_{0}}}+{\frac {V_{1}-V_{M}}{R_{1}}}+{\frac {V_{2}-V_{M}}{R_{2}}}+\cdot \cdot \cdot +{\frac {V_{n}-V_{M}}{R_{n}}}$

Développons :

$0={\frac {V_{0}}{R_{0}}}-{\frac {V_{M}}{R_{0}}}+{\frac {V_{1}}{R_{1}}}-{\frac {V_{M}}{R_{1}}}+{\frac {V_{2}}{R_{2}}}-{\frac {V_{M}}{R_{2}}}+\cdot \cdot \cdot +{\frac {V_{n}}{R_{n}}}-{\frac {V_{M}}{R_{n}}}$

${\frac {V_{0}}{R_{0}}}+{\frac {V_{1}}{R_{1}}}+{\frac {V_{2}}{R_{2}}}+\cdot \cdot \cdot +{\frac {V_{n}}{R_{n}}}={\frac {V_{M}}{R_{0}}}+{\frac {V_{M}}{R_{1}}}+{\frac {V_{M}}{R_{2}}}+\cdot \cdot \cdot +{\frac {V_{M}}{R_{n}}}$

${\frac {V_{0}}{R_{0}}}+{\frac {V_{1}}{R_{1}}}+{\frac {V_{2}}{R_{2}}}+\cdot \cdot \cdot +{\frac {V_{n}}{R_{n}}}=V_{M}\cdot \left({\frac {1}{R_{0}}}+{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdot \cdot \cdot +{\frac {1}{R_{n}}}\right)$

On peut alors calculer le potentiel au niveau du nœud :

$V_{M}={\frac {{\frac {V_{0}}{R_{0}}}+{\frac {V_{1}}{R_{1}}}+{\frac {V_{2}}{R_{2}}}+\cdot \cdot \cdot +{\frac {V_{n}}{R_{n}}}}{{\frac {1}{R_{0}}}+{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdot \cdot \cdot +{\frac {1}{R_{n}}}}}$

Loi de Millman proprement dite

Image du théorème de Millman

Cela permet de calculer les tensions et courants dans les circuits similaires à celui présenté à votre droite. Il comprend plusieurs branches, chacune avec un générateur et une résistance (un récepteur linéaire, en toute généralité). Le courant qui passe dans une branche $M$ est égal à la somme de tous les autres courants.

$I_{M}=\sum _{i}{\frac {E_{i}}{R_{i}}}$

La tension s'obtient à partir du courant en multipliant par la résistance équivalente des autres branches (ou en divisant par la conductance équivalente).

$U_{M}=\sum _{i}{\frac {E_{i}}{R_{i}}}\cdot R_{eq}={\frac {\sum _{i}{\frac {E_{i}}{R_{i}}}}{G_{eq}}}$

Vu que ces branches sont en parallèle, on a : ${\frac {1}{R_{eq}}}=\sum _{i}{\frac {1}{R_{i}}}$, ou encore $G_{eq}=\sum _{i}G_{i}$, ce qui donne :

$U_{M}=\sum _{i}{\frac {E_{i}}{R_{i}}}\cdot \sum _{i}G_{i}={\frac {\sum _{i}{\frac {E_{i}}{R_{i}}}}{\sum _{i}{\frac {1}{R_{i}}}}}$

Exemple

Millman Illustration exemple

Prenons le circuit à votre droite. La loi de Millman permet de calculer la tension entre les points a et b. L'application de la loi de Millman donne :

$V_{ab}={\frac {{\dfrac {V_{1}}{R_{1}}}+{\dfrac {V_{2}}{R_{2}}}+{\dfrac {V_{3}}{R_{3}}}}{{\dfrac {1}{R_{1}}}+{\dfrac {1}{R_{2}}}+{\dfrac {1}{R_{3}}}}}$ $={\frac {{\dfrac {10}{5}}+{\dfrac {0}{8}}+{\dfrac {-12}{3}}}{{\dfrac {1}{5}}+{\dfrac {1}{8}}+{\dfrac {1}{3}}}}=-3V$

Les théorèmes de Thévenin et Norton

Les théorèmes de Thévenin et de Norton, que nous allons voir dans ce qui suit, sont souvent appelés les théorèmes des générateurs. La raison est qu'ils permettent de remplacer un (morceau de) circuit linéaire par un dipôle équivalent à un générateur linéaire. Plus précisément, ils permettent de remplacer un circuit linéaire, ou une partie de circuit linéaire, par un générateur couplé avec une résistance. Cela n'est évidemment possible que si le circuit est localisé entre deux points d'un circuit, à savoir si ce (morceau de) circuit possède deux bornes.

Le théorème de Thévenin

Exemple d'application du théorème de Thévenin. On voit que le circuit de gauche, vu entre deux points, est équivalent au circuit de droite composé d'un générateur en série avec une résistance. On peut remplacer le circuit de droite par celui de gauche, et réciproquement, sans changer la physique ou les calculs lors de l'étude du circuit.

Le théorème de Thévenin dit qu'un (morceau de) circuit linéaire est équivalent à un générateur de tension en série avec une résistance. La tension produite par le générateur est appelé la tension de Thévenin et la résistance associée est appelée la résistance de Thévenin. La tension du générateur se calcule en prenant le circuit ouvert, alors que la résistance se calcule en remplaçant les générateurs par leur résistance interne.

Pour en donner un exemple, étudions le circuit ci-dessous, noté (a) dans le schéma. Celui-ci est composé de quatre résistances et d'un générateur, avec une charge entre les points A et B.

• Première étape : calculer la tension de Thévenin. Pour cela, on prend le circuit ouvert : on ne met rien entre les points A et B. On calcule alors la tension entre A et B : celle-ci est la tension de Thévenin. Cette étape est illustrée au schéma noté (b). Dans l'exemple étudié, un simple diviseur de tension suffit. Le calcul donne :

$U_{Thevenin}=U_{gen}\cdot {\frac {R3+R2}{R2+R3+R4}}=15V\cdot {\frac {1k\Omega +1k\Omega }{1k\Omega +1k\Omega +2k\Omega }}=7,5V$

• Seconde étape : calculer la résistance de Thévenin. Pour cela, on remplace les générateurs par leur résistance interne et on calcule la résistance équivalente du circuit. Cette étape est illustrée au schéma noté (c). On voit que R1 est en série avec un circuit composé de R4 en parallèle avec R2 et R3 (qui sont en série). Pour commencer, R2 et R3 sont en série, ce qui fait que leurs résistances s'additionnent. Puis, on doit calculer la résistance équivalente à R4 en parallèle avec R3 + R2, ce qui donne :

$R_{temp}={\frac {R4\cdot (R3+R2)}{R4+R3+R2}}=1k\Omega$

Reste à calculer la résistance équivalente totale qui est égale à la résistance précédente mise en série avec R1. l'addition donne :

$R_{eq}=2k\Omega$

• Une fois cela fait, on peut remplacer le circuit par un générateur qui produit la tension calculée à la première étape, mis en série avec la résistance calculée à la seconde étape.

Exemple d'application du théorème de Thévenin.

Le théorème de Norton

Exemple d'application du théorème de Norton. On voit que le circuit de gauche, vu entre deux points, est équivalent au circuit de droite composé d'un générateur en parallèle avec une résistance. On peut remplacer le circuit de droite par celui de gauche, et réciproquement, sans changer la physique ou les calculs lors de l'étude du circuit.

Le théorème de Norton dit qu'un (morceau de) circuit linéaire est équivalent à un générateur de courant en parallèle avec une résistance. Le courant produit par le générateur est appelé le courant de Norton et la résistance associée est appelée la résistance de Norton. Le courant se calcule en court-circuitant le circuit étudié, à savoir en reliant les deux bornes du (morceau de ) circuit. Par contre, la résistance se calcule en remplaçant les générateurs par leur résistance interne et en calculant la résistance équivalente du circuit obtenu.

Exemple d'application du théorème de Norton.

Pour mieux comprendre, voici un exemple d'application.

Nous allons étudier le circuit numéroté (a), illustré dans le schéma ci-contre, à gauche.

• Première étape : calculer le courant de Norton. Pour cela, on court-circuite le circuit complet, en mettant un fil entre A et B. Il reste alors à calculer le courant qui circule dans ce fil, qui n'est autre que le courant de Norton. Dans l'exemple ci-dessous, le court-circuit donne le circuit numéro (b). On obtient alors un circuit proche du diviseur de courant, et les calculs donnent :

$I_{Norton}=1,82A$

• Seconde étape : remplacer les générateurs par des fils et calculer la résistance équivalente entre A et B. Le circuit obtenu en remplaçant les générateurs est illustré à gauche : c'est le numéro (c). Les calculs donnent une résistance équivalente égale à 3,66 Ohms.

$R_{Norton}=3,66\Omega$

• Enfin, on peut remplacer le circuit complet par un générateur qui produit le courant calculé à la première étape, en parallèle avec la résistance calculée à la seconde étape.

Conversion entre Thévenin et Norton

On a vu dans le chapitre sur les générateurs qu'il est possible de passer d'un générateur de Thévenin à un générateur de Norton assez facilement. Rappelons simplement les faits suivants :

• Les deux résistances, de Norton et de Thévenin, sont identiques. En effet, elles se calculent de la même manière : ce sont toutes deux la résistance équivalente entre les points A et B, une fois les générateurs remplacés par leur résistance interne.
• Le courant de Norton et la tension de Thévenin sont reliés entre eux par l'équation suivante, où $R_{Eq}$ est la résistance équivalente mentionnée précédemment.

$I_{cc}={\frac {U_{vide}}{R_{Eq}}}$

Le théorème de Kennelly et les transformations étoile-mesh

La transformation étoile-mesh permet de passer d'un ensemble de résistances « en étoile » vers un ensemble « en mesh». Les deux configurations sont illustrées ci-dessous. Dans la configuration en étoile, plusieurs résistances sont reliées à un point central commun. Une extrémité de chaque résistance est connectée au point central, l'autre extrémité est "libre". L'ensemble des extrémités libres forme un polygone. Dans la configuration en mesh, chaque résistance relie deux sommets du polygone.

Transformation étoile-mesh.

Le passage de la configuration en étoile vers la configuration en mesh utilise l'équation suivante. Elle donne la valeur de la résistance entre deux points A et B du polygone, qui est notée $R_{ab}$. Pour cela, elle a besoin de la somme de toutes les résistances de l'étoile, notée $\sum R_{i}$, de la valeur de la résistance qui connecte A au centre ($R_{a}$) et la valeur de la résistance qui connecte B au centre ($R_{b}$). On a alors :

$R_{ab}={\frac {R_{a}\cdot R_{b}}{\sum R_{i}}}$

La transformation inverse, d'un mesh vers une étoile, n'est pas possible dans que l'on impose des contraintes additionnelles. Cela signifie qu'il n'y a pas de formule générale qui permette de faire les calculs. La raison est que la transformation d'une étoile vers un mesh augmente le nombre de résistance, alors que la transformation inverse le réduit. Autant calculer un grand nombre de résistances à partir d'un plus petit nombre ne pose pas de problème, autant calculer un petit nombre de résistances à partir de plus de résistances est bien moins facile.

On peut deviner facilement que la transformation étoile-mesh fait passer de $N$ résistances à $N(N+1) \over 2$ résistances.

Un cas particulier : le théorème de Kennelly

L'application du théorème précédent dans le cas à trois résistances s'appelle le théorème de Kennelly. Il permet de passer d'un ensemble de résistances « en étoile » vers un ensemble « en triangle ». Dans la configuration en étoile, trois résistances sont reliées à un point central commun. Dans la configuration en triangle, elles sont reliées de manière à former un triangle. Les deux configurations sont illustrées ci-dessous. Le théorème de Kennelly est aussi appelé la transformation étoile-triangle. Précisons que dans ce cas particulier, on peut faire la conversion dans les deux sens : de l'étoile vers le mesh, mais aussi du mesh vers l'étoile. C'est possible parce que, dans les deux cas, le nombre de résistances est conservé : il y a trois résistances dans les deux configurations. Pour comprendre comment passer de l'une à l'autre, nous allons utiliser les deux circuits ci-dessous, avec les résistances numérotées.

Théorème de Kennelly.

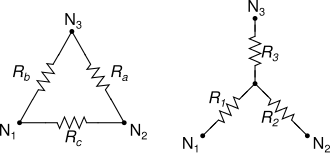
Le passage de la configuration en triangle vers la configuration en étoile utilise les trois équations suivantes :

$R_{1}={\frac {R_{b}\cdot R_{c}}{R_{a}+R_{b}+R_{c}}}$

$R_{2}={\frac {R_{a}\cdot R_{c}}{R_{a}+R_{b}+R_{c}}}$

$R_{3}={\frac {R_{a}\cdot R_{b}}{R_{a}+R_{b}+R_{c}}}$

Le passage de la configuration en étoile vers la configuration en triangle utilise les trois équations suivantes :

$R_{a}={\frac {R_{1}\cdot R_{2}+R_{2}\cdot R_{3}+R_{3}\cdot R_{1}}{R_{1}}}$

$R_{b}={\frac {R_{1}\cdot R_{2}+R_{2}\cdot R_{3}+R_{3}\cdot R_{1}}{R_{2}}}$

$R_{c}={\frac {R_{1}\cdot R_{2}+R_{2}\cdot R_{3}+R_{3}\cdot R_{1}}{R_{3}}}$

Ce théorème est utile pour simplifier certains circuits assez complexes. Deux exemples d'utilisation de ce théorème sont illustrés ci-dessous. On voit, dans ces deux exemples, que le théorème de Kennelly permet de passer d'un circuit assez complexe à un circuit plus simple à interpréter.

Exemple d'utilisation du théorème de Kennelly.

Exemple d'utilisation du théorème de Kennelly.