Photographie/Netteté des images/Profondeur de champ/Considérations théoriques

PHOTOGRAPHIE Un wikilivre pour ceux qui veulent apprendre la photographie de façon méthodique et approfondie. Enrichissez-le en mettant votre propre savoir à la disposition de tous. Si vous ne savez pas où intervenir, utilisez cette page. Voyez aussi le « livre d'or ». Aujourd'hui 25/12/2024, le Wikilivre de photographie comporte 7 160 articles

plan du chapitre en cours Netteté des images photographiques Généralités (A) Pouvoir séparateur des objectifs (B) Fonction de transfert de modulation (B) Les émulsions et la reproduction des détails (BC) Netteté des images numériques (AB) L'œil et la perception de la netteté (B) Profondeur de champ (B) Importance des conditions d'observation des photographies Questions générales et intérêt esthétique Considérations théoriques Considérations pratiques Le « bokeh » (B) Le flou de bougé Systèmes de stabilisation (B) Niveau A - débutant B - lecteur averti C - compléments Avancement Projet Ébauche des chapitres En cours Avancé Terminé Quoi de neuf Docteur ? ajouter une rubrique les 10 dernières mises à jour notables Southworth & Hawes (2 mars) Showa Optical Works (29 février) Bradley & Rulofson (4 janvier, MàJ) - - - - - - - - - - Lucien Lorelle (10 décembre, MàJ) Groupe des XV (10 décembre) MàJ de la liste des APN Sony (10 décembre) Alfred Stieglitz (17 novembre) Classement et archivage (12 novembre) ADOX (24 août) Hippolyte Bayard (22 août) mises à jour précédentes Famille Chevalier (opticiens) (22 août) Ronald Kroon (8 août) Giorgio Sommer (27 juillet) Frank Jay Haynes (22 juillet) Oliver Wendell Holmes Sr. (6 juin) Paul Rudolph (26 mai) Sabine Weiss (1er juillet) Frédéric Boissonnas (10 février) Ariel Varges (8 février) Andreas Gursky (9 janvier) Antonio Esplugas Puig (8 janvier) Cosina CS-3 (7 janvier) Cosina CS-2 (7 janvier) Cosina CS-1 (7 janvier) Cosina CT-1 (7 janvier) Vivitar XV-2 (7 janvier) Fujica AX-3 (7 janvier) Mamiya ZE (7 janvier) G. Lékégian (3 janvier) Vivitar Zoom Thyristor 285 (3 janvier) Sunpak Autozoom 3600 (2 janvier) National PE-3057 (2 janvier) Minolta Auto 320X (2 janvier) Mamiyalite ZE (2 janvier) Konica X-24 Auto (2 janvier) Fujica Auto Strobo 300 X (2 janvier) Contax TLA 20 (2 janvier) Pierre Jaffeux (2 janvier) Archives 2016 2015 2014 2013 2012 2011 2010 2009 2008

navigation rapide Fabricants et marques de produits et de matériels A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Ca.a CZ Ep Fu Ko.a.f Le Mi Ni.a Ol Pa Pe Ri Sa Si So Ta Personnalités du monde de la photographie A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Éditeurs de cartes postales photographiques A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Thèmes ▪ Bibliographie Glossaire ▪ Formulaires ▪ Modèles pour le livre cliquez sur les titres ci-dessous pour dérouler les menus ■  préface - SOMMAIRE COMPLET Préface SOMMAIRE COMPLET ■  notions fondamentales et conseils pour les débutants Les premiers pas Conseils aux débutants ■  aspects esthétiques, thèmes photographiques Choix esthétiques Perspective Composition des images Thèmes ■  références scientifiques Mathématiques Physique-Chimie Rayonnements électromagnétiques ■  photométrie, colorimétrie, optique Photométrie L’œil et la vision humaine Colorimétrie Optique ■  appareils, objectifs, éclairage, accessoires, entretien Appareils Objectifs Éclairage Mesure de la lumière, posemètres Filtres optiques Matériel de laboratoire Accessoires Préparation et entretien du matériel et des objectifs Fabricants et marques ■  procédés chimiques Procédés anciens Émulsions argentiques, généralités Surfaces sensibles Traitements en général Traitements argentiques monochromes Traitements couleurs Traitements divers Sensitométrie Tirage des épreuves ■  procédés numériques Acquisition des images L'image numérique Logiciels Impression des photographies ■  caractéristiques physiques des images, densité, netteté Densitométrie Netteté des images ■  compléments techniques et pratiques Techniques scientifiques Techniques particulières Conditions particulières de prise de vues Finition et présentation des photographies Classement et archivage Installations photographiques ■  photographie et vie sociale, histoire, enseignement,institutions, droit... Histoire de la photographie Droit de la photographie Enseignement Métiers de la photographie Institutions, fondations, musées Manifestations publiques Salons Sociétés, organisations, éditeurs Prix et distinctions Photographie commerciale ■  personnalités A B C D E F G H I J K L M N O P Q R S T U V W X Y Z ■  glossaire A B C D E F G H I J K L M N O P Q R S T U V W X Y Z ■  annexes Bibliographie Modèles pour les pages Textes en attente

Cher lecteur, on peut comprendre que les chiffres vous bassinent, comme dirait le contrepéteur fou.

Pour autant, ne négligez pas la lecture de cette page. Vous pouvez passer outre les calculs, mais prenez le temps de lire les conclusions !

Dans toute étude théorique, il convient de prendre des précautions, faute de quoi tout résultat devient critiquable. Nous allons donc commencer par poser avec soin les hypothèses sur lesquelles reposent les calculs.

Hypothèses, définitions, calculs et démonstrations

Hypothèses générales pour les calculs

• Nous ne considèrerons ici que les causes de flou qui interviennent au moment de la prise de vue et relèvent des lois de l'optique géométrique. Il est bien entendu qu'en pratique, les causes de dégradation des images sont cumulatives ; toute perte de netteté équivaut une réduction apparente de la profondeur de champ.

• L'objectif sera considéré comme une lentille mince parfaite et donc capable de donner d'une source ponctuelle, à toutes les ouvertures, une image elle aussi ponctuelle. Les lecteurs courageux retrouveront exactement les mêmes résultats en utilisant non plus le centre optique d'une lentille mince, mais les points nodaux d'un système centré. Notons aussi que plus la qualité d'un objectif est élevée, plus les calculs de profondeur de champ sont fiables.

• Pour les images numériques, nous supposerons en outre que le capteur est d'une qualité suffisante pour utiliser au mieux l'image fournie par l'objectif et que par ailleurs les images n'ont subi, avant leur enregistrement, aucun traitement susceptible de modifier leur netteté apparente.

• Les images finales seront examinées a priori depuis la distance orthoscopique. Nous verrons en temps utile ce que cela donne dans les autres cas.

Nous utiliserons par ailleurs les formules des lentilles simples convergentes sous leur forme arithmétique et non sous leur forme algébrique. D'une part, le fait que les objectifs donnent des images inversées n'influe aucunement sur la netteté, d'autre part certains appareils sont munis d'objectifs de type « périscopique » et dans ce cas le signe du grandissement perd toute signification. Nous n'aurons en fait besoin que de deux formules :

• la relation de conjugaison : ${\frac {1}{p}}+{\frac {1}{p'}}={\frac {1}{f}}$

$p\,$ est la distance de l'objet au centre optique, $p'\,$ la distance de l'image au centre optique et $f\,$ la distance focale de l'objectif

• et la formule du grandissement : $g={\frac {p'}{p}}$

il s'agit bien sûr du rapport des dimensions de l'image à celles correspondantes de l'objet

• en éliminant p entre les deux formules, on trouve : $p'=f\,(g+1)\,$

Gros « coup de gueule » en passant

Attention ! Il faut se méfier au plus haut point du jargon pseudo-scientifique répandu à toutes les époques par certains photographes désireux de passer pour des savants aux yeux d'un public naïf. La notion de « cercle de confusion », que vous rencontrerez très souvent dans la plupart des magazines et dans les mauvais ouvrages de vulgarisation, où elle n'est du reste jamais clairement définie, en est un des exemples les plus caractéristiques !

Hélas, cette sottise continue de se répandre à la manière d'un virus, à cause de la paresse intellectuelle des gratte-papier successifs qui, au lieu de revenir aux sources, se contentent de reproduire à la façon des perroquets ce qu'ils ont lu ici ou là et que d'autres avaient déjà mille fois recopié de la même manière imbécile.

Disons-le tout net : l'usage du « cercle de confusion » complique tous les calculs et tous les raisonnements, en semant partout... la confusion, pour la simple raison que l'acuité visuelle correspond à un angle, pas à une longueur. Il ne s'agit donc pas seulement d'un intermédiaire de calcul inutile mais bien plutôt d'un concept fondamentalement nuisible.

Sans regret,

expédions le cercle de confusion à la poubelle et refermons bien le couvercle !

Tolérance de mise au point, profondeur de foyer, profondeur de champ

Dans tous les schémas ci-dessous, la lumière va de la gauche vers la droite, du sujet vers la surface sensible.

Avant d'aborder l'étude détaillée de ces diverses notions, il est nécessaire de bien poser le problème !

Conventions et notations Un objectif parfait muni d'un diaphragme de diamètre d fait correspondre aux points lumineux R, P et A leurs images respectives R', P' et A'. Le cône d'ouverture $\epsilon \,$ indique la limite angulaire de netteté admise : les détail des images vus depuis O sous un angle inférieur ou égal à $\epsilon \,$ sont considérés comme nets.
Les points R', P' et A' sont les conjugués respectifs des points R, P et A. On se rappellera que depuis le point O, on voit sous le même angle chaque élément du sujet et son image.
Mise au point exacte D'un objet plan perpendiculaire en P à l'axe optique, l'objectif fournit une image plane sur le plan de la surface sensible situé en P'. Tous les points de cette image sont vus sous un angle très inférieur à $\epsilon \,$ et la photographie a partout sa netteté maximale.
Remarque : La mise au point exacte n'est possible, dans des conditions habituelles et avec un objectif parfaitement corrigé, que si le sujet est plan et perpendiculaire à l'axe optique. La « bascule » permet d'étendre l'obtention de la netteté à des sujets plans non perpendiculaires à cet axe. Il existe aussi des objectifs spéciaux qui permettent de former sur un plan l'image d'objets convexes ou concaves.
Tolérance de mise au point Ici l'objet se trouve en P mais la mise au point est faite sur A. La surface sensible est donc en A' et reçoit l'image de P sous la forme d'une tache tout juste contenue dans le cône de netteté. Le même raisonnement vaut pour R et R' ; nous trouvons que la distance de la surface sensible au centre optique peut varier de OR' à OA' sans que la dégradation de l'image dépasse la limite fixée. Pour obtenir une image nette de P, la mise au point peut donc être faite à n'importe quelle distance entre A et R.
En pratique, la mise au point peut se trouver hors tolérance pour de multiples raisons : mauvais calage des systèmes de visée ou des objectifs, films mal guidés, « autofocus » pénalisé par une lumière trop faible, etc. Sur beaucoup d'appareils, le système « autofocus » ne fonctionne pas de façon continue mais par paliers, de sorte que la mise au point exacte n'est presque jamais obtenue.
Profondeur de foyer La mise au point est faite sur P où se trouve l'objet. La surface sensible devrait théoriquement se trouver en P' mais en fait elle peut occuper n'importe quelle position entre A' et P' sans que la tache-image soit vue sous un angle qui dépasse la limite choisie $\epsilon \,$.
La profondeur de foyer est généralement très faible et il faut donc respecter des tolérances de fabrication très précises au niveau des boîtiers et des montures d'objectifs. Dans les appareils reflex elle intervient deux fois, pour la mise en position de la surface sensible et pour celle du dépoli de visée. Les constructeurs doivent également prendre des dispositions pour assurer le maintien du film dont les défauts de planéité provoqueraient l'apparition de zones floues, s'ils étaient supérieurs à la profondeur de foyer.
Profondeur de champ La mise au point est faite sur P et la surface sensible se trouve donc en P' mais l'objet n'est plus plan. Des points de cet objet tels que A et R donnent des taches-images dont le diamètre reste acceptable ; l'image de tout objet à trois dimensions situé entre les plans perpendiculaires à l'axe optique passant par A et R sera nette.
Nous arrivons là au cœur du problème ...
Conjugaison de la profondeur de champ et de la profondeur de foyer Il résulte de ce qui précède que la profondeur de champ et la profondeur de foyer constituent deux espaces conjugués ; par conséquent toute modification de l'une entraîne ipso facto une modification de l'autre.
Deux remarques s'imposent maintenant : Si le diamètre du diaphragme diminue, les cônes formés par les faisceaux lumineux sont moins ouverts, la profondeur de foyer A' R' et la profondeur de champ A R augmentent ensemble. Le diaphragme est donc un organe de mise au point puisqu'il agit directement sur l'étendue de la zone de netteté. Nous n'allons pas tarder à y revenir. Dans l'immense majorité des cas, l'image obtenue sur la surface sensible lors de la prise de vue est plus petite ou beaucoup plus petite que le sujet photographié ; la profondeur de champ est alors beaucoup plus étendue que la profondeur de foyer. Dans le domaine de la macrophotographie proprement dite, c'est l'inverse qui se produit : l'image originale est plus grande que l'objet photographié, la profondeur de champ devient plus petite que la profondeur de foyer ... et ça change tout !

Calcul de la profondeur de foyer

Définition

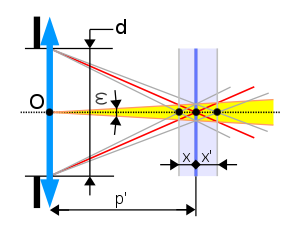
On appelle profondeur de foyer la zone de l'espace dans laquelle doit se trouver la surface sensible pour que l'image d'un objet plan perpendiculaire à l'axe optique et sur lequel on a fait la mise au point puisse être considérée comme nette.

Les rayons lumineux issus de P convergent en P' en formant un faisceau d'autant plus ouvert que le diamètre d du diaphragme est plus important. Si le plan de la pellicule ou du capteur n'est pas placé exactement en P', l'image enregistrée ne sera pas un point mais une petite tache circulaire. Celle-ci sera néanmoins perçue comme nette si elle est vue depuis O sous un angle au plus égal à ε.

Le plan du film peut être avancé d'une distance $x\,$ ou reculé d'une distance $x'\,$ sans que l'image soit altérée de façon visible.

pour en savoir plus : consulter le détail du calcul

Les valeurs de $x\,$ et $x'\,$ sont telles que :

$x={\frac {\epsilon \,f\,(g+1)^{2}\,n}{1+\epsilon \,(g+1)\,n}}\qquad et\qquad x'={\frac {\epsilon \,f\,(g+1)^{2}\,n}{1-\epsilon \,(g+1)\,n}}$

$n\,$ est l'ouverture relative du diaphragme.

Ces formules complètes ne sont en fait intéressantes que dans certains cas particuliers car le produit $\epsilon \,(g+1)\,n$ est presque toujours très petit devant 1. Si par exemple le rapport de grandissement est 2, l'ouverture relative 16 et la limite de netteté angulaire 1/1 500, on trouve :

$\epsilon (g+1)n={\frac {1}{1\;500}}\cdot 3\cdot 16={\frac {48}{1\;500}}=0,032$

La limite de netteté n'est évidemment pas définie à 3 % près, on utilisera donc le plus souvent une forme simplifiée :

$x\approx x'\approx \epsilon \,n\,f\,(g+1)^{2}$

Pour une netteté donnée, l'intervalle dans lequel doit se trouver le plan de la pellicule ou du capteur est toujours d'autant plus petit que la focale est plus courte, le grandissement plus faible et le diaphragme plus ouvert.

Si la mise au point est faite très loin ou a fortiori à l'infini, alors le grandissement est très faible ou nul et la formule se simplifie encore :

$x\approx x'\approx \epsilon \,n\,f$

Exemple : on veut photographier un objet situé à l'infini ou très loin (g = 0) avec un objectif de focale 50 mm ouvert à f/2 et une limite de flou tolérée de 1/1 500 radian :

$x={\frac {2\cdot 50}{1\;500}}={0,066\,mm}$

Toutes choses égales par ailleurs, un réglage du diaphragme à f/22 donnerait x = 0,7 mm, une valeur bien moins contraignante.

On comprend mieux dès lors pourquoi les appareils doivent être construits avec une grande précision, en particulier s'ils comportent une visée reflex ou un capteur de petit format derrière un objectif de courte focale. Le maintien de la planéité des pellicules photographiques est également, depuis toujours, un souci pour les constructeurs. Pour beaucoup d'usages scientifiques, la limite de netteté de 1/1 500 peut être considérée comme très insuffisante. Les exigences de précision se trouvent évidemment renforcées et il va de soi qu'il faut alors utiliser un matériel de très haute qualité.

Calcul de la profondeur de champ

Nous disposons désormais de tous les éléments qui vont nous permettre d'entrer dans le vif du sujet. Les diverses distances des objets et des images au centre optique de la lentille seront notées OA = a, OA' = a', OP = p, etc. La mise au point est faite sur le point P et la surface sensible est calée très exactement au niveau du point P' où convergent les rayons issus de P.

• Les rayons issus d'un point extrême R, qui correspond à la limite éloignée de profondeur de champ, convergent en R' et poursuivent leur course jusqu'à la surface sensible où ils forment une tache de diamètre $\epsilon \,p'$.

• Les rayons issus d'un point extrême A, qui correspond à la limite proche de profondeur de champ, convergeraient en A' s'ils n'étaient pas interceptés par la surface sensible, sur laquelle ils forment eux aussi une tache de diamètre $\epsilon \,p'$.

Avec les appareils compacts numériques, qui utilisent des capteurs minuscules associés à des objectifs de courte focale, ce diamètre est très faible ; les performances des objectifs et des capteurs doivent être du meilleur niveau .... Si p' vaut par exemple 12 mm, avec une limite de netteté de 1/1 500, on obtient :

$\epsilon \,p'={\frac {12}{1\;500}}=0,008\,mm=8\,\mu m$

La portion de l'espace comprise entre les deux plans perpendiculaires à l'axe optique qui passent par A et R sera susceptible de fournir une image nette compte tenu des critères adoptés pour le calcul. L'espace qui sépare ces deux plans correspond à la profondeur de champ. Cette profondeur varie énormément avec le diaphragme, elle peut être quasi nulle si l'objectif est lumineux et grand ouvert et considérable s'il est fermé au maximum.

pour en savoir plus : consulter le détail du calcul

Évaluation de la profondeur de champ

On considère un objectif de focale $f\,$ mis au point à la distance $p\,$, avec une ouverture relative du diaphragme $n\,$. Les deux distances extrêmes qui limitent la zone de netteté s'écrivent :

$a=OA={\frac {pf}{f+\epsilon pn}}\qquad et\qquad r=OR={\frac {pf}{f-\epsilon pn}}$

Ce calcul permet de vérifier que l'appareil est correctement réglé. Notons que le dénominateur de $r\,$ peut s'annuler ou devenir négatif, ce qui n'a plus de sens. Si tel est le cas, pas de panique, cela signifie simplement que la zone de netteté s'étend jusqu'à l'infini. Nous y reviendrons un peu plus loin.

Calcul de la distance de mise au point et de l'ouverture du diaphragme

Question : comment dois-je régler mon appareil pour que la netteté s'étende de la distance $a\,$ à la distance $r\,$ ?

Réponse : en calculant la bonne distance de mise au point et la bonne ouverture du diaphragme !

$p={\frac {2\,a\,r}{(a+r)}}\qquad et\qquad n={\frac {f(r-a)}{2\,a\,r\,\epsilon }}$

Remarques :

1. Vous lirez probablement ici ou là que la profondeur de champ est répartie pour un tiers devant le plan de mise au point et deux tiers derrière. En réalité, elle s'étend toujours davantage derrière que devant mais pas en proportions fixes : en macrophotographie, les profondeurs avant et arrière sont presque égales mais pour le paysage, quand la netteté s'étend jusqu'à l'infini, la zone arrière est ... infiniment plus grande que la zone avant. Même si elle est très grossièrement vérifiée pour des applications comme le portrait ou le nu en studio, la répartition 1/3 - 2/3 n'est qu'un cas particulier : mieux vaut donc oublier cette « loi » qui n'en est pas une.
2. Lorsque l'on fait la mise au point à faible distance et que l'on utilise un objectif complexe, l'origine des distances n'est pas facile à situer. C'est en particulier le cas pour la plupart des objectifs « macro » modernes, qui sont en fait des objectifs à focale variable.
3. Vous trouverez peut-être dans d'autres ouvrages des formules un peu différentes, dans lesquelles les distances sont comptées non pas à partir du centre optique (ou du point nodal objet) mais à partir du plan du film. Cela ne change rien en pratique pour les sujets éloignés mais si on les applique sans tenir compte du changement d'origine, ces formules donnent des résultats complètement faux en photographie rapprochée.

Exemple de calcul

On veut photographier un sujet dont les divers éléments intéressants sont compris entre 1,5 m et 3 m, avec un objectif de focale 50 mm (0,05 m) et une limite angulaire de netteté de 1/1 500.

$p={\frac {2\cdot 1,5\cdot 3}{1,5+3}}=2\,m\qquad et\qquad n={\frac {0,05(3-1,5)1\;500}{2\cdot 1,5\cdot 3}}=12,5$

Une ouverture plus grande ne permettra pas d'obtenir la netteté optimale de tous les éléments du sujet. En fermant davantage, d'autres éléments présents dans le cadre, particulièrement ceux de l'arrière-plan, risquent de sembler nets et de perturber la vision ; de plus, on augmentera la diffraction. Le diaphragme apparaît donc bien comme un instrument de mise au point !

Faut-il un ordinateur pour faire ce calcul ? Non, si l'objectif est muni d'une échelle de profondeur de champ, ce qui n'est évidemment pas le cas avec les équipements de bas de gamme et l'immense majorité des appareils compacts numériques !

De part et d'autre du losange qui sert de repère pour les échelles de distance et de diaphragme, on voit des traits symétriques portant des valeurs de diaphragme, 4, 8 et 16. En tournant la bague de mise au point de façon que les repères 1,5 m et 3 m soient symétriques par rapport au losange, comme par miracle, on fait la mise au point sur ... 2 m. De plus, nos deux repères se trouvent ... quelque part entre les graduations d'ouverture 11 (nombre non gravé) et 16. Avec 12,5, notre calcul n'est apparemment pas si mauvais. Nous expliquerons plus loin ce petit « miracle ».

Distance hyperfocale

La profondeur de champ s'étend normalement entre une limite proche et une limite lointaine. Que se passe-t-il lorsque la seconde se trouve rejetée à l'infini ?

Reprenons les formules.

$a={\frac {p\,f}{f+\epsilon \,p\,n}}\qquad et\qquad r={\frac {p\,f}{f-\epsilon \,p\,n}}$

$r\,$ tend vers l'infini lorsque :

$f-\epsilon \,p\,n=0$

soit :

$f=\epsilon \,p\,n$

Le report de $f\,$ dans la première équation donne de suite :

$a={\frac {p}{2}}$

Finalement :

$p=2a\qquad et\qquad n={\frac {f}{2a\epsilon }}$

On peut aussi écrire les formules qui donnent $a\,$ et $r\,$ sous la forme suivante :

${\frac {1}{a}}={\frac {1}{p}}+{\frac {\epsilon \,n}{f}}\qquad et\qquad {\frac {1}{r}}={\frac {1}{p}}-{\frac {\epsilon \,n}{f}}$

Par convention, on appelle distance hyperfocale la quantité :

$h={\frac {f}{\epsilon \,n}}$

Contrairement à la focale, cette distance ne caractérise pas un objectif donné, mais un ensemble de trois paramètres qui sont la focale, l'ouverture du diaphragme et le degré de netteté choisi arbitrairement (ce qui ne veut pas dire au hasard !).

La valeur de l'hyperfocale est facile à estimer avec les objectifs qui possèdent des graduations de profondeur de champ. Il suffit de tourner la bague de mise au point sur l'infini pour en lire la valeur en face de l'ouverture relative. Par exemple, sur ce Summicron de 50 mm, on trouve environ 5 m à f/16, 10 m à f/8, etc. Ces valeurs peuvent être retrouvées facilement à partir de la limite de netteté angulaire généralement admise par les fabricants, c'est-à-dire 1/1 500.

Les formules qui donnent la profondeur de champ peuvent s'écrire en fonction de l'hyperfocale :

$a={\frac {p\,h}{h+p}}\qquad et\qquad r={\frac {p\,h}{h-p}}$

On peut aussi les écrire sous une forme qui n'est pas sans rappeler la formule de Snell-Descartes, mais cette analogie est purement formelle :

${\frac {1}{a}}={\frac {1}{p}}+{\frac {1}{h}}\qquad et\qquad {\frac {1}{r}}={\frac {1}{p}}-{\frac {1}{h}}$

Il en résulte que si la netteté doit s'étendre d'une distance a jusqu'à l'infini,

• la première chose à faire est de régler la mise au point sur 2a
• la seconde est de déterminer l'ouverture du diaphragme en fonction du degré de netteté souhaité.

Avec un objectif de 50 mm de focale (0,05 m), une profondeur de champ s'étendant de 5 m à l'infini et une limite de netteté de 1/1 500, nous ferons la mise au point sur 10 m et nous adopterons pour le diaphragme :

$n={\frac {0,05\cdot 1\;500}{10}}=7,5\approx 8$

C'est bien ce que nous lisons sur notre échelle de profondeur de champ :

En passant au diaphragme 16, nous pouvons diviser les distances par 2 et donc obtenir, avec une mise au point sur 5 m, une netteté qui s'étendra de 2,5 m jusqu'à l'infini.

Lorsque nous mettons au point sur l'infini, la netteté commence à l'hyperfocale. Sur l'échelle de profondeur de champ de notre objectif, h se lit directement en face des graduations du diaphragme.

On lit 5 m à 16, 10 m à 8 et, en prolongeant la série, on déduit 20 m à 4 ou 40 m à 2, ouverture maximale de cet objectif.

Au diaphragme 16, mise au point faite sur l'infini, la netteté commence à 5 m. En mettant au point sur 5 m, elle s'étend de 2,5 m à l'infini. Le fait de mettre au point sur l'infini est presque toujours une erreur et constitue, d'une certaine manière, un « gaspillage » des possibilités de l'objectif . Pour un paysage, par exemple, l'œil est très exigeant pour la netteté des objets situés à quelques mètres ou dizaines de mètres mais beaucoup plus tolérant pour celle des lointains, ce qui rend encore plus logique une mise au point au voisinage de l'hyperfocale.

Un préréglage de la mise au point sur l'hyperfocale a permis à beaucoup de grands photographes, par le passé, de gagner un temps précieux lorsqu'ils prenaient des photos sur le vif, notamment pour les photographies de rue : ils n'avaient ainsi plus besoin de se préoccuper de la mise au point. Aujourd'hui, cette notion est toujours utile aux photographes qui ont l'habitude d'opérer avec un appareil non automatique ou avec un automatisme à priorité diaphragme : même si l'appareil se charge de la mise au point, le fait de fixer le diaphragme pour disposer dans tous les cas d'une profondeur de champ suffisante améliore les chances de réussite.

Les appareils à mise au point fixe sont réglés une fois pour toute sur l'hyperfocale qui correspond à la plus grande ouverture de leur diaphragme. Il faut donc s'attendre à ce qu'ils donnent leurs moins mauvais résultats à des distances de l'ordre de 3 à 5 m.

Profondeur de champ et distance focale

Un peu partout, dans beaucoup de livres et dans la plupart des revues, dans les pages des sites internet, on affirme que la profondeur de champ dépend de la distance de mise au point, du diaphragme et de la distance focale, en oubliant presque toujours au passage cet autre facteur essentiel qu'est le format de la surface sensible.

Les formules mathématiques qui permettent de calculer la profondeur de champ montrent que celle-ci varie avec la distance focale puisque, toutes choses égales par ailleurs, les distances $a\,$ et $r\,$ en dépendent. En pratique, pourtant, c'est presque toujours faux ! Cet aspect des choses est examiné en détail dans le chapitre suivant, consacré aux considérations pratiques sur ce thème.

Profondeur de champ et format de la surface sensible

Lorsque l'on a choisi un point de vue et un cadrage, le format de la surface sensible impose la distance focale de l'objectif. En « prenant la décision qui s'impose », un responsable politique ne fait que subir les événements et ne décide, en réalité, rien du tout. Ici c'est pareil, on prend la focale qui s'impose !

Le choix du point de vue et du cadrage relève de critères pratiques (accessibilité par exemple) et esthétiques, de la volonté de montrer certaines choses et d'en cacher d'autres, etc. ; en revanche, il faut remonter au choix du format de la surface sensible si l'on veut comprendre pourquoi « la profondeur de champ dépend de la focale sans en dépendre ».

La distance focale est déterminée par le format de la surface sensible et le point de vue

Depuis un point de vue donné O, nous pouvons prendre des photographies composées de la même façon sur des surfaces sensibles de dimensions très différentes, par exemple, sur un capteur électronique de 6 x 8 mm ou sur un plan-film de 24 x 30 cm.

$H\,$ est une dimension de référence de l'objet (choisie perpendiculaire à l'axe optique) et $h\,$ la dimension correspondante d'une des images prise comme exemple. La distance de mise au point $p\,$ et l'angle $\alpha \,$ sous lequel on voit l'objet sont tous deux fixés par le choix du point de vue. La distance $p'\,$ de l'objectif à la surface sensible est directement proportionnelle aux dimensions de cette dernière. Le grandissement est déterminé par la composition de l'image et il est lui aussi directement proportionnel aux dimensions de la surface sensible :

$g={\frac {h}{H}}={\frac {p'}{p}}$

La focale de l'objectif est alors imposée par les relations de conjugaison habituelles :

$f={\frac {p\,p'}{p+p'}}={\frac {p^{2}\,g}{p+p\,g}}={\frac {p\,g}{1+g}}$

Cette formule peut être simplifiée lorsque l'on est loin du sujet car le grandissement est alors très petit et on le néglige devant 1.

$f\approx pg=p'$

Exemple 1

Lors de la photographie d'une nature morte en studio, le centre optique de l'objectif se trouve à 60 cm d'un objet de 250 mm de hauteur. L'image de cet objet doit mesurer 40 mm sur un négatif 6x6 cm. Quelle focale faut-il théoriquement utiliser ?

$g={\frac {40}{250}}=0,16\qquad \rightarrow \qquad f={\frac {600\times 0,16}{1+0,16}}=82,8mm$

Si l'on ne dispose pas de d'un objectif à focale variable, on peut adopter un objectif de focale un peu plus courte, ce qui oblige à découper l'image par la suite ; cela revient à utiliser un format utile plus petit que le format réel.

Exemple 2

On photographie depuis une distance p = 50 m un arbre de hauteur H = 10 m, de telle façon que celui-ci donne une image de 20 mm sur la surface sensible. Attention aux unités !

$f\approx pg=p'=p\times {\frac {h}{H}}=50\;000{\frac {20}{10\;000}}=100\,mm$

La profondeur de champ varie avec le format de la surface sensible

La distance focale étant imposée par les conditions de prise de vue, ce sont désormais ces dernières qui vont entrer en ligne de compte dans les formules donnant la profondeur de champ. Ainsi, en remplaçant $f\,$ par sa valeur en fonction de $g\,$,

$a={\frac {p\,f}{f+\epsilon \,p\,n}}={\frac {p{\frac {p\,g}{1+g}}}{{\frac {p\,g}{1+g}}+\epsilon \,p\,n}}={\frac {p\,g}{g+\epsilon \,n(1+g)}}={\frac {p}{1+\epsilon \,n({\frac {1}{g}}+1)}}$

et

$r={\frac {p\,f}{f-\epsilon \,p\,n}}={\frac {p{\frac {p\,g}{1+g}}}{{\frac {p\,g}{1+g}}-\epsilon \,p\,n}}={\frac {p\,g}{g-\epsilon \,n\,(1+g)}}={\frac {p}{1-\epsilon \,n\,({\frac {1}{g}}+1)}}$

$a={\frac {p}{1+\epsilon \,n({\frac {1+g}{g}})}}\qquad et\qquad r={\frac {p}{1-\epsilon \,n({\frac {1+g}{g}})}}$

ou encore :

$a={\frac {p}{1+\epsilon \,n+{\frac {\epsilon \,n}{g}}}}\qquad et\qquad r={\frac {p}{1-\epsilon \,n-{\frac {\epsilon \,n}{g}}}}$

Lorsque le grandissement est très faible on peut le négliger devant 1 :

si g est petit :     $a={\frac {p}{1+{\frac {\epsilon \,n}{g}}}}\qquad et\qquad r={\frac {p}{1-{\frac {\epsilon \,n}{g}}}}$

Les distances $a\,$ et $r\,$ qui définissent l'étendue de la profondeur de champ dépendent directement du grandissement et donc des dimensions de l'image qui se forme sur la surface sensible, mais pas de la focale. On remarque aussi que lorsque le grandissement augmente, les dénominateurs des fractions se rapprochent 1 et donc que $a\,$ et $r\,$ se rapprochent de $p\,$, la profondeur de champ diminue.

• la profondeur de champ diminue lorsque le format de la surface sensible augmente, et inversement,

• elle ne dépend pas de la distance focale.

Il faut bien reconnaître que la variation de profondeur de champ avec le format ne saute pas aux yeux à l'examen des formules. Celles-ci ne sont pas toujours faciles à utiliser, surtout lorsque le sujet est éloigné. C'est probablement pour cette raison que les rédacteurs d'articles de vulgarisation ne s'aventurent guère sur ce terrain.

Dans le cas de $r\,$ la zone de netteté s'étend jusqu'à l'infini lorsque le dénominateur devient nul, ce qui se produit par exemple lorsque le diaphragme est suffisamment fermé :

$g=\epsilon \,n\,(1+g)\qquad \rightarrow \qquad n={\frac {g}{\epsilon \,(1+g)}}$

Attention ! Il ne faut jamais oublier que le grandissement se calcule à partir du plan de mise au point, même si le sujet principal est situé à une distance différente.

Exemple 3

Nous photographions un arbre de hauteur H = 10 m depuis une distance p = 50 m de telle façon qu'il donne une image de 20 mm sur une pellicule de 24 x 36 mm. Le diaphragme est fixé à 5,6 et la limite de netteté à 1/1 500 ; quelle est l'étendue de la profondeur de champ ?

Nous pouvons utiliser ici pour a la formule approchée puisque le grandissement qui vaut 20/10 000 = 0,002 est très petit par rapport à 1 :

$a={\frac {p\,g}{g+\epsilon \,n}}={\frac {50\;000\times 0,002}{0,002+{\frac {5,6}{1\;500}}}}={\frac {100}{0,002+0,003\;733}}\approx 17\;500\,mm=17,5\,m$

Le diaphragme minimum pour que la netteté s'étende jusqu'à l'infini est $n={\frac {g}{\epsilon }}=0,002\times 1\;500=3$

Il est donc inutile de calculer r puisque nous avons une ouverture relative de 5,6 ; la netteté s'étendra donc de 17,5 m à l'infini.

Échangeons maintenant notre appareil contre un moyen format 6 x 9 cm. En respectant les mêmes proportions, l'image de l'arbre mesurera cette fois 50 mm et le grandissement sera 0,005. Avec la même ouverture relative de diaphragme, nous aurons :

$a={\frac {p\,g}{g+\epsilon \,n}}={\frac {50\;000\times 0,005}{0,005+{\frac {5,6}{1\;500}}}}={\frac {250}{0,005+0,003\;733}}\approx 17\;500\,mm=28,6\,m$

et $r={\frac {p\,g}{g-\epsilon \,n}}={\frac {50\;000\times 0,005}{0,005-{\frac {5,6}{1\;500}}}}={\frac {250}{0,005-0,003\;733}}\approx 197\;400\,mm=197,4\,m$

La profondeur de champ sera très nettement réduite et s'étendra donc d'environ 30 m à 200 m.

Exemple 4

Nous photographions un personnage assis de hauteur 1,2 m ; l'appareil au format 24 x 36 est situé à 3 m du modèle, le diaphragme est réglé sur 8 et nous voulons que l'image mesure 24 mm, soit un grandissement de 0,02 que nous continuerons de négliger devant 1.

$a={\frac {p\,g}{g+\epsilon \,n}}={\frac {3\;000\times 0,02}{0,02+{\frac {8}{1\;500}}}}={\frac {60}{0,02+0,005\;333}}\approx 2\;370\,mm\approx 2,4\,m$

$r={\frac {p\,g}{g-\epsilon \,n}}={\frac {3\;000\times 0,02}{0,02-{\frac {8}{1\;500}}}}={\frac {60}{0,02-0,005\;333}}\approx 4\;090\,mm=4,1\,m$

La profondeur de champ va de 2,4 à 4,1 m et s'étend donc sur 1,7 m, il ne devrait pas y avoir de problème.

Passons au format 6x9 cm. L'image a cette fois une hauteur de 60 mm et le grandissement passe à 0,05

$a={\frac {pvg}{g+\epsilon \,n}}={\frac {3\;000\times 0,05}{0,05+{\frac {8}{1\;500}}}}={\frac {150}{0,05+0,005\;333}}\approx 2\;710\,mm\approx 2,7\,m$

$r={\frac {p\,g}{g-\epsilon \,n}}={\frac {3\;000\times 0,05}{0,05-{\frac {8}{1\;500}}}}={\frac {150}{0,05-0,005\;333}}\approx 3\;360\,mm=3,35\,m$

La profondeur de champ s'étend maintenant de 2,7 à 3,35 m, soit 0,65 m seulement, elle devient beaucoup moins confortable.

Ces deux exemples expliquent pourquoi les habitués du 24x36 qui décident un beau matin de passer au moyen format ou à la chambre éprouvent souvent les pires difficultés avec la profondeur de champ, avant de changer leurs habitudes de travail. Ce n'est pas par hasard que les chambres de grand format sont munies d'objectifs dont les diaphragmes affichent des valeurs aussi élevées que f/32, f/45, f/64, voire f/90, couramment utilisées en paysage par des photographes tels qu'Ansel Adams.

Nous suggérons au lecteur de déterminer la valeur de l'ouverture du diaphragme qui permet d'obtenir une netteté convenable entre 2 m et l'infini, avec une chambre de 24 x 30 cm et un objectif de 400 mm de focale...

Exemple 5

Un insecte de longueur 12 mm, situé à 100 mm du centre optique de l'objectif, est photographié sur du film 24 x 36 de façon que son image mesure 24 mm, soit les deux tiers de la longueur du format. Le diaphragme a été réglé à 16 et la netteté est toujours fixée à 1/1 500. Quelle est la profondeur de champ disponible ?

Nous voici dans le domaine de la macrophotographie, puisque l'image obtenue à la prise de vue est plus grande que l'objet. Le grandissement vaut 2 et il faut donc appliquer les formules complètes :

${\frac {1+g}{g}}={\frac {3}{2}}=1,5$

$a={\frac {100}{1+{\frac {16}{1\;500}}1,5}}={\frac {100}{1+0,016}}=98,4mm$

$r={\frac {100}{1-{\frac {16}{1\;500}}1,5}}={\frac {100}{1-0,016}}=101,6mm$

la profondeur de champ n'atteint que 3,2 mm, ce qui risque fort de ne pas suffire pour avoir une photographie parfaitement nette de la bestiole.

Supposons maintenant que sans changer de point de vue, nous utilisions un appareil compact numérique équipé d'un « gros » capteur de 12 x 9 mm. Avec les mêmes proportions que précédemment l'image de l'insecte mesure cette fois 8 mm seulement, le grandissement n'est plus que de 2/3 et nous ne sommes plus dans le domaine de la macrophotographie...

${\frac {1+g}{g}}=2,5$

$a={\frac {100}{1+{\frac {16}{1\;500}}2,5}}={\frac {100}{1+0,026\;67}}=97,4mm$

$r={\frac {100}{1-{\frac {16}{1\;500}}2,5}}={\frac {100}{1-0,026\;67}}=102,7mm$

La profondeur de champ atteint cette fois 5,3 mm, ce n'est pas le grand luxe mais nous avons gagné 67 % par rapport au cas précédent et nos chances de réussite sont bien meilleures !

Avec un capteur encore plus petit de 6 x 8 mm, toujours en conservant le même point de vue et donc le même cadrage, la profondeur de champ passe à 7 mm, soit plus du double de la valeur obtenue en 24 x 36.

• En agrandissant au même format les trois images et en les observant à la même distance, nous constaterions que si le cadrage n'a pas changé, il n'en va pas de même pour l'étendue de la zone de netteté !

• En calculant les distances focales correspondant aux trois prises de vue, nous trouverions respectivement 66,7 mm, 40 mm et 31 mm ; en conservant le cadrage, la focale diminue moins vite que le format de la surface sensible.

• Avec du film, la diminution exagérée du format de prise de vue pose de nombreux problèmes : le grain et les divers défauts de l'émulsion, les risques de rayures, etc. dégradent très fortement la qualité de l'image. Les conditions ont changé avec l'apparition des capteurs numériques de petit format, liée à une augmentation considérable mais discrète de la qualité des objectifs qui sont de plus petite taille et plus faciles à fabriquer.

Beaucoup de photographes amateurs de diapositives et de photographie rapprochée ont eu comme une sorte de révélation en troquant leur reflex argentique contre un appareil compact numérique tel que le Coolpix 4500 de Nikon, attribuant à tort l'augmentation quasi miraculeuse de leur taux de réussite aux vertus du « numérique » et oubliant l'effet du changement de format. Après avoir une nouvelle fois cassé leur tirelire pour s'offrir un reflex numérique muni d'un grand capteur, beaucoup ont alors été très étonnés de retrouver soudain les problèmes qu'ils connaissaient quelques temps auparavant en 24x36...

Netteté des images photographiques Généralités (A) Pouvoir séparateur des objectifs (B) Fonction de transfert de modulation (B) Les émulsions et la reproduction des détails (BC) Netteté des images numériques (AB) L'œil et la perception de la netteté (B) Profondeur de champ (B) Importance des conditions d'observation des photographies Questions générales et intérêt esthétique Considérations théoriques Considérations pratiques Le « bokeh » (B) Le flou de bougé Systèmes de stabilisation (B)