Le noyau atomique/L'interaction nucléaire

Il n'est pas rare de trouver des nucléons isolés, en dehors de tout noyau, mais ce n'est pas la norme. La plupart se trouvent dans des noyaux atomiques et il faut fournir de l'énergie pour les en séparer. De plus, les nucléons ont naturellement tendance à s'assembler en noyaux atomiques s'ils sont très proches. Ce phénomène est assez similaire, dans les grandes lignes, à la formation d'un atome à partir de noyaux et d'électrons. Dans le cas de l'atome, c'est la force électromagnétique qui fait qu'électrons et noyaux s'attirent au point de s'assembler en atomes. Pour la formation d'un noyau à partir de nucléons, c'est presque la même chose : les nucléons s'attirent au point de s'assembler en noyaux.

Sauf que pour la formation des noyaux, l'interaction électromagnétique n'est pas en cause : les neutrons ne sont pas influencés par cette interaction, sans compter que les protons se repoussent vu qu'ils sont de même charge électrique. La gravité n'est pas non plus en cause : le calcul nous dit que les masses des nucléons sont trop faibles. On est bien obligé d'admettre qu'il existe une autre force qui attire les nucléons entre eux, la force nucléaire. Celle-ci agit sur les nucléons et quelques particules semblables nommées hadrons.

La force nucléaire

De nombreuses expériences ont donné des indications précieuses pour comprendre la force nucléaire. La plupart de ces expériences sont des expériences de collision entre nucléons : on fait entrer deux nucléons en collision et on regarde ce qui se passe. Avec un peu de chance et des conditions optimales, la collision donne naissance à un noyau composé de deux nucléons. On peut aussi faire entrer en collision un noyau avec un nucléon et le faire grossir petit à petit, ce qui donne des indications sur la force nucléaire. Enfin, des expériences d’interférométrie de nucléons ont aussi été utilisées dans ce but. Mais concentrons-nous pour le moment sur ce que ces expériences nous ont appris sur la force nucléaire.

Les propriétés statiques de la force nucléaire

L'expérience montre que la force nucléaire peut être aussi bien attractive que répulsive : tout dépend de la distance entre les deux nucléons. Quand les deux nucléons sont extrêmement proches, la force nucléaire est fortement répulsive. Mais si les deux particules sont "loin", la force nucléaire est attractive. Ce comportement est assez inédit, mais a des implications assez importantes. En premier lieu, le caractère attractif à longue distance permet aux nucléons de se condenser en noyaux : les nucléons éloignés s'attirent et ont donc tendance à se regrouper en noyaux. Une conséquence du caractère répulsif à courte distance est que le noyau atomique est presque incompressible : rapprocher deux nucléons demande une force énorme pour surcompenser la force nucléaire.

Expérimentalement, la force nucléaire se moque de la nature des nucléons : à distance égale, cette force sera identique entre deux neutrons, deux protons, ou entre un proton et un neutron. Cette propriété est appelée l'indépendance à la charge de la force nucléaire.

Une des difficultés pour mettre en question la force forte est sa dépendance au spin. Pour le dire simplement, la force forte entre deux nucléons n'est pas la même selon que leurs spins sont alignés ou non. La force forte est bien plus forte quand deux nucléons ont leurs spins alignés dans le même sens, que quand leurs spins sont opposés.

La relation force-distance

Graphique qui montre plusieurs résultats expérimentaux concernant la force nucléaire en fonction de la distance au nucléon.

Comme vous le savez peut-être, la plupart des forces est assez bien approximé par une force centrale, à savoir une force convergeant/divergeant d'un point central. La force nucléaire est aussi une force centrale, en première approximation. En clair, un nucléon est la source d'une force qui converge vers lui et/ou diverge de lui. Pour une force centrale, l'intensité de la force dépend uniquement de la distance. Pour la gravité et l'électricité, la force est proportionnelle au carré de la distance, par exemple. Mais pour la force nucléaire, la relation distance-force n'est pas linéaire, ni même proportionnelle au carré de la distance. La relation est beaucoup plus compliquée, mais elle est globalement bien illustrée ci-contre.

Déjà, comme dit plus haut, la force nucléaire est répulsive à courte distance, mais attractive sur les longues distances. Ensuite, sur les longues distances, la force nucléaire diminue exponentiellement avec la distance. En conséquence, la force nucléaire diminue plus vite que la force électromagnétique sur les longues distances. À partir d'une certaine distance, la répulsion entre protons sera plus forte que la force nucléaire. Les physiciens en déduisent que les noyaux avec un grand nombre de protons peuvent plus facilement se briser ou perdre des nucléons. Certains pensent même qu'il existe une limite maximale au nombre de protons dans un noyau ou au rapport entre protons et neutrons.

Précisons que la force nucléaire n'est pas exactement une force centrale : si elle est bien approximée par une force centrale, des déviations apparaissent à haute énergie et des termes non-centraux doivent être ajoutés aux équations. C'est aussi le cas de la gravité et de l'électricité : autant la loi de la gravitation de Newton est une bonne approximation, autant la relativité générale va plus loin que la simple loi en 1/r². Dans le cas de la force nucléaire, on peut la décomposer en trois termes distincts :

• une force centrale, répulsive à courte distance et attractive à longue distance ;
• une force tensorielle, qui dépend de l'orientation des spins des nucléons ;
• une force spin-orbite, qui dépend du mouvement des spins l'un par rapport à l'autre.

Le potentiel nucléaire

La force nucléaire a des points communs assez forts avec la gravité, le magnétisme et l'électricité. Notamment, ces forces proviennent chacune d'une source : objet massif pour la gravité, charge électrique pour l'électricité, aimant pour le magnétisme, et nucléon pour la force nucléaire. De plus, ces forces fournissent une énergie potentielle aux objets sur lesquels elles agissent. Vous avez peut-être déjà entendu parler de l'énergie potentielle de gravitation/de pesanteur, ou encore de l'énergie potentielle électrostatique. Eh bien la même chose existe pour l'énergie nucléaire. Chaque nucléon influence les nucléons environnants en leur fournissant une énergie potentielle nucléaire, qui dépend de la distance avec la source (mais pas que). La force nucléaire vient du fait que les nucléons tentent de minimiser leur énergie potentielle et se déplacent vers l'endroit où elle est la plus faible, c’est-à-dire proche du nucléon à l'origine du potentiel. La forme du potentiel, à savoir sa relation avec la distance du nucléon, est illustrée avec le graphique suivant, qui montre la valeur du potentiel entre deux nucléons, exprimée en fonction de la distance qui les sépare.

Illustration du potentiel nucléaire (simplifié). On voit qu'il existe une distance idéale, qui minimise l'énergie des nucléons (notée Rmin), mais aussi une distance minimale liée au fait que les nucléons ne peuvent pas s'interpénétrer. Il existe une différence d'énergie (notée epsilon) entre un nucléon totalement libre, non-soumis à la force nucléaire, et un nucléon à la distance idéale.

L'énergie potentielle totale est impossible à calculer à l'heure actuelle (début 2016), même si diverses théories en donnent une approximation convenable. On sait que la force nucléaire est une sorte de résidu de la force qui s'exerce entre les quarks et les gluons. Les quarks d'un même nucléon s'attirent entre eux, mais les spécificités de la force forte font que cette attraction déborde quelque peu des nucléons. Le résultat est qu'il apparaît une force nucléaire entre nucléons. Une théorie complète de la force nucléaire doit donc être dérivée de la chromodynamique quantique, la théorie qui décrit l'interaction forte, les quarks et les gluons. Mais certaines théories se passent de ce genre de fioritures et donnent des développements plus simples à comprendre.

Les modèles descriptifs du potentiel nucléaire central

Comme dit plus haut, la force nucléaire est la somme de plusieurs forces, donc de plusieurs potentiels différents. Le potentiel nucléaire est la somme d'un potentiel central, d'un potentiel tensoriel et d'un potentiel spin-orbite. Le potentiel s'écrit donc :

$U(r)=U_{\text{central}}(r)+U_{\text{spin-orbite}}+U_{\text{tensor}}({\vec {r}})$

Une bonne approximation du potentiel nucléaire est de dire qu'il est constant dans tout le noyau, sauf en périphérie où il diminue très rapidement avec la distance. La formule de Saxon-Woods donne une bonne approximation du potentiel nucléaire, avec :

• $U_{central}(r)$ le potentiel central et $U_{central}(0)$ est le potentiel central au centre du noyau ;
• $r$ est la distance par rapport au centre du noyau ;
• $R$ est le rayon du noyau, dans la partie où le potentiel est constant ;
• $l$ est la longueur sur laquelle le potentiel chute rapidement en périphérie.

$U_{\text{central}}(r)={\frac {U_{\text{central}}(0)}{1+e^{\frac {r-R}{l}}}}$

Une autre approximation est donnée par le potentiel de Reid, à savoir la formule suivante :

$U_{\text{Reid}}(r)=-10.463\cdot {\frac {e^{-\mu r}}{\mu r}}-1650.6\cdot {\frac {e^{-4\mu r}}{\mu r}}+6484.2\cdot {\frac {e^{-7\mu r}}{\mu r}}$

Le couplage spin-orbite

Les deux formules précédentes décrivent correctement le potentiel central, mais laissent de côté les deux autres composantes. Mais les potentiels centraux ne permettent pas de décrire correctement l'interaction nucléaire, même en première approximation. Il faut leur ajouter une composante tensorielle, ainsi qu'un couplage spin-orbite. Si l'on peut négliger la composante tensorielle, en première approximation, ce n'est pas le cas de la composante spin-orbite. L'interaction nucléaire dépend si fortement des spins des nucléons que l'on doit la prendre en compte dans un modèle complet. La composante spin-orbite est approximativement égale à :

$U_{\text{spin-orbite}}=k(r)\cdot \left({\vec {L}}\cdot {\vec {S}}\right)$, avec ${\vec {L}}$ le moment cinétique orbital d'un nucléon et ${\vec {S}}$ le spin du nucléon. Le terme $k(r)$ est une fonction des coordonnées dans le noyau.

On peut calculer facilement le terme ${\vec {L}}\cdot {\vec {S}}$ en partant de la définition du moment cinétique total. Pour rappel, celui-ci est la somme du spin et du moment cinétique orbital :

${\vec {J}}={\vec {S}}+{\vec {L}}$

Élevons le tout au carré :

${\vec {J}}^{2}=\left({\vec {S}}+{\vec {L}}\right)^{2}={\vec {S}}^{2}+{\vec {L}}^{2}+2{\vec {L}}\cdot {\vec {S}}$

On réorganise les termes :

${\vec {L}}\cdot {\vec {S}}={\frac {1}{2}}\left({\vec {J}}^{2}-{\vec {S}}^{2}-{\vec {L}}^{2}\right)$

Rappelons que du fait de la quantification de l'énergie, on a $|J|^{2}=\hbar ^{2}j(j+1)$, $|S|^{2}=\hbar ^{2}s(s+1)$ et $|L|^{2}=\hbar ^{2}l(l+1)$, ce qui donne :

${\vec {L}}\cdot {\vec {S}}={\frac {\hbar ^{2}}{2}}\left(j(j+1)-s(s+1)-l(l+1)\right)$

On sait que $s=\pm {\frac {1}{2}}$, on a $j=l\pm {\frac {1}{2}}$. En injectant dans l'équation précédente, on a :

${\vec {L}}\cdot {\vec {S}}={\frac {l}{2}}$, pour $j=l+{\frac {1}{2}}$

${\vec {L}}\cdot {\vec {S}}=-{\frac {l+1}{2}}$, pour $j=l-{\frac {1}{2}}$

On voit que le potentiel spin-orbite dépend donc de la valeur du spin, et qu'il peut prendre deux valeurs différentes selon le spin. La différence d'énergie entre l'état de spin $s=+{\frac {1}{2}}$ et l'état $s=-{\frac {1}{2}}$ se calcule en soustrayant les deux équations précédentes et en multipliant par le potentiel de base. Cela donne :

$\Delta E=\hbar ^{2}\left(l+{\frac {1}{2}}\right)U_{{\vec {L}}\cdot {\vec {S}}}$

La théorie de Yukawa

Illustration de la théorie de Yukawa. On voit que des processus ayant lieu à l'intérieur des nucléons donnent naissance à des mésons (des pions, des kaons et bien d'autres particules), qui passent d'un nucléon à l'autre. L'émission et l'absorption d'un de ces mésons transfère de l'énergie et de la quantité de mouvement du nucléon émetteur au nucléon récepteur, ce qui induit une attraction ou une répulsion.

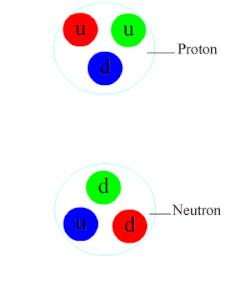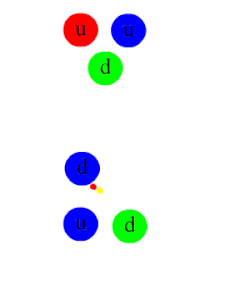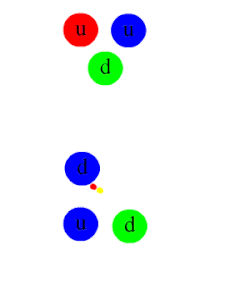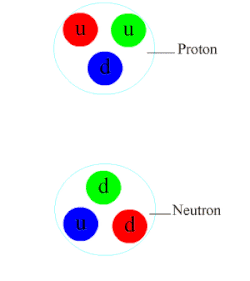
Historiquement, le premier modèle du potentiel nucléaire crée par un nucléon a été inventé par Yukawa en 1935. Selon sa théorie, le nucléon source émet des particules qui servent d'intermédiaires pour la force nucléaire. Quand un nucléon environnant absorbe ces particules intermédiaires, il est attiré ou repoussé du nucléon source. La particule intermédiaire possède de plus une masse, ce qui fait que la force induite a une portée assez limitée. En élaborant cette idée dans le cadre de la physique quantique, Yukawa trouva la formule suivante pour le potentiel, où g est une constante, m est la masse de la particule intermédiaire et r est la distance entre les deux nucléons.

$V=-{\frac {g^{2}}{4\pi }}{\frac {e^{-mr}}{r}}$

Dans le cas particulier où $m=0$, on retrouve le potentiel en $1 \over r$ d'interaction électrostatique (la loi de Coulomb) et du potentiel gravitationnel. Pour la force nucléaire forte et faible, le coefficient $m$ est plus important, ce qui fait que le potentiel nucléaire ne suit pas une loi en $1 \over r$, mais chute plus vite, d'où le fait que la force nucléaire est une force à courte-distance. Ci-dessous, on montre le potentiel en fonction de la distance r, pour diverses valeurs de m. On voit que plus m est grand, plus le potentiel de Yukawa se concentre sur de courtes distances.

Comparaison entre le potentiel nucléaire de Yukawa et le potentiel électrostatique.

Potentiel de Yukawa en fonction de la distance, pour diverses valeurs de m.

Après la publication de la théorie de Yukawa, les physiciens se mirent en quête de la particule intermédiaire. Les premiers soupçons se portèrent sur des particules comme le méson pion, le méson rho, le méson sigma, le méson oméga, etc. Mais les propriétés de ces particules donnaient une force nucléaire soit totalement attractive, soit totalement répulsive : aucune ne donnait une force nucléaire attractive à longue distance et répulsive à faible distance. De nos jours, on pense qu'il existerait plusieurs types de particules intermédiaires. La répulsion à courte distance provient des mésons rho et sigma, l'attraction à courte distance provient des mésons oméga, et l'attraction à longue distance provient des mésons phi (les pions).

La constante de couplage de la QCD

La formule de Yukawa peut se scinder en deux parties : un terme ${\frac {g^{2}}{4\pi }}$ qui détermine la puissance de la force, et un second terme ${\frac {e^{-mr}}{r}}$ qui décrit comment elle évolue avec la distance. Le premier terme est proportionnel à ce qu'on appelle la constante de couplage de l'interaction nucléaire forte, un paramètre qui détermine la puissance de cette force, l'amplitude de ses effets sur la matière. Plus elle est forte, plus l'interaction est importante. La constante de couplage vaut, par définition :

$\alpha _{s}={\frac {g^{2}}{4\pi \hbar c}}$

La théorie quantique nous dit que si la constante de couplage est assez faible, proche de 1, l'interaction est alors assez faible. Sous cette condition, elle peut être approximée par des techniques dites perturbatives. En utilisant ces techniques, on peut formuler la plupart des équations en utilisant les puissances de g, ce qui rend le traitement mathématique assez simple et les approximations faciles. Mais dans le cas de la force forte, la constante de couplage est bien plus grande que 1 et ces techniques ne sont pas applicables. À vrai dire, c'est pour cela qu'on l'appelle la force forte : sa constante de couplage est très importante.

La constante de couplage dépend de l'énergie des nucléons interagissant

La constante de couplage porte mal son nom. La réalité est que si elle décrit bien un couplage entre deux particules, elle n'est pas constante. Elle varie en fonction de l'énergie des particules interagissantes. Le graphique ci-dessous illustre l'évolution de la constante de couplage en fonction de l'énergie. On voit qu'elle diminue avec l'énergie.

Paramètre g en fonction de l'énergie.

Constante de couplage en fonction de l'énergie.

Vous remarquerez que la constante de couplage diminue de manière logarithmique avec l'énergie. Cela signifie que plus on fournit d'énergie à des nucléons, moins l'interaction forte entre eux sera forte. An fournissant suffisamment d'énergie à deux nucléons, on peut en théorie les séparer. À longue distance, deux nucléons ne vont presque pas interagir. Par contre, à courte distance, la force forte sera importante et elle suffira à condenser les nucléons en noyaux. L'évolution logarithmique de la constante de couplage a des conséquences assez intéressantes, mais très techniques à expliquer.

$\alpha _{s}(k^{2})\approx {\frac {g_{0}^{2}}{\ln \left(k^{2}/\Lambda ^{2}\right)}}$