Fonctionnement d'un ordinateur/Les portes logiques
Le chapitre précédent nous a appris à encoder des nombres en binaire, ce qui est suffisant pour encoder n'importe quelle donnée. Reste à savoir comment un ordinateur fait des opérations sur ces bits. UDans ce chapitre, nous allons voir qu'un ordinateur effectue des opérations très simples sur des bits, opérations qui sont implémentées avec des portes logiques, elles-mêmes fabriquées avec des transistors. Nous allons voir les portes logiques dans ce chapitre, puis comment faire des circuits plus complexes dans les chapitres suivants.
Les portes logiques de base
[modifier | modifier le wikicode]Les portes logiques sont des circuits qui prennent un ou plusieurs bits en entrée et fournissent un bit en guise de résultat. Elles possèdent des entrées sur lesquelles on va placer des bits, et une sortie sur laquelle se trouve le bit de résultat. Les entrées ne sont rien d'autre que des morceaux de « fil » conducteur sur lesquels on envoie un bit (une tension). La sortie est similaire, si ce n'est qu'on récupère le bit de résultat.
- Sur les schémas qui vont suivre, les entrées des portes logiques seront à gauche et les sorties à droite !
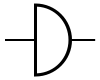
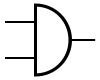
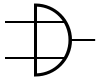
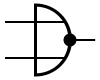
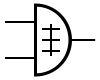
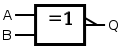
Les portes logiques ont différent symboles selon le pays et l'organisme de normalisation :
- Commission électrotechnique internationale (CEI) ou International Electrotechnical Commission (IEC),
- Deutsches Institut für Normung (DIN, Institut allemand de normalisation),
- American National Standards Institute (ANSI).
La porte OUI/BUFFER
[modifier | modifier le wikicode]La première porte fondamentale est la porte OUI, qui agit sur un seul bit : sa sortie est exactement égale à l'entrée. En clair, elle recopie le bit en entrée sur sa sortie. Pour simplifier la compréhension, je vais rassembler les états de sortie en fonction des entrées pour chaque porte logique dans un tableau que l'on appelle table de vérité.
Mine de rien, la porte OUI est parfois utile. Elle sert surtout pour recopier un signal électrique qui risque de se dissiper dans un fil trop long. On place alors une porte OUI au beau milieu du fil, pour éviter tout problème, la porte logique régénérant le signal électrique, comme on le verra dans le chapitre suivant. Cela lui vaut parfois le nom de porte BUFFER, ce qui veut dire tampon. Les portes OUI sont aussi utilisées dans certaines mémoires RAM (les mémoires SRAM), comme nous le verrons dans quelques chapitres.
La porte NON
[modifier | modifier le wikicode]La seconde porte fondamentale est la porte NON, qui agit sur un seul bit : la sortie d'une porte NON est exactement le contraire de l'entrée. Son symbole ressemble beaucoup au symbole d'une porte OUI, la seule différence étant le petit rond au bout du triangle.
La porte ET
[modifier | modifier le wikicode]La porte ET possède plusieurs entrées, mais une seule sortie. Cette porte logique met sa sortie à 1 quand toutes ses entrées valent 1.
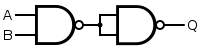
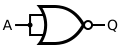
La porte NAND
[modifier | modifier le wikicode]La porte NAND donne l'exact inverse de la sortie d'une porte ET. En clair, sa sortie ne vaut 1 que si au moins une entrée est nulle. Dans le cas contraire, si toutes les entrées sont à 1, la sortie vaut 0.
Au fait, si vous regardez le schéma de la porte NAND, vous verrez que son symbole est presque identique à celui d'une porte ET : seul un petit rond (blanc pour ANSI, noir pour DIN) ou une barre (CEI) sur la sortie de la porte a été rajouté. Il s'agit d'une sorte de raccourci pour schématiser une porte NON.
La porte OU
[modifier | modifier le wikicode]La porte OU est une porte dont la sortie vaut 1 si et seulement si au moins une entrée vaut 1. Dit autrement, sa sortie est à 0 si toutes les entrées sont à 0.
La porte NOR
[modifier | modifier le wikicode]La porte NOR donne l'exact inverse de la sortie d'une porte OU.
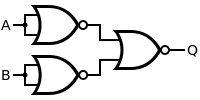
La porte XOR
[modifier | modifier le wikicode]Avec une porte OU, deux ET et deux portes NON, on peut créer une porte nommée XOR. Cette porte est souvent appelée porte OU exclusif. Sa sortie est à 1 quand les deux bits placés sur ses entrées sont différents, et vaut 0 sinon.
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
La porte XNOR
[modifier | modifier le wikicode]La porte XOR possède une petite sœur : la XNOR. Sa sortie est à 1 quand les deux entrées sont identiques, et vaut 0 sinon (elle est équivalente à une porte XOR suivie d'une porte NON).
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Interlude propédeutique : combien il y a-t-il de portes logiques différentes ?
[modifier | modifier le wikicode]Les portes logiques que nous venons de voir ne sont pas les seules. En fait, il existe un grand nombre de portes logiques différentes, certaines ayant plus d'intérêt que d'autres. Mais avant toute chose, nous allons parler d'un point important : combien y a-t-il de portes logiques en tout ? La question a une réponse très claire, pour peu qu'on précise la question. Les portes que nous avons vu précédemment ont respectivement 1 et 2 bits d'entrée, mais il existe aussi des portes à 3, 4, 5, bits d’entrée, voire plus. Il faut donc se demander combien il existe de portes logiques, dont les entrées font N bits. Par exemple, combien y a-t-il de portes logiques avec un bit d'entrée ? Avec deux bits d'entrée ? Avec 3 bits ?
Pour cela, un petit raisonnement peut nous donner la réponse. Vous avez vu plus haut qu'une porte logique est définie par une table de vérité, qui liste le bit de sortie pour chaque combinaison possible des entrées. Le raisonnement se fait en deux étapes. La première détermine, pour n bits d'entrée, combien il y a de lignes dans la table de vérité. La seconde détermine combien de tables de vérité à c lignes existent.

Le nombre de lignes de la table de vérité se calcule facilement quand on se rend compte qu'une porte logique reçoit en entrée un "nombre" codé sur n bits, et fournit un bit de résultat qui dépend du "nombre" envoyé en entrée. Chaque ligne de la table de vérité correspond à une valeur possible pour le "nombre" envoyé en entrée. Pour n bits en entrée, la table de vérité fait donc lignes.
Ensuite, calculons combien de portes logiques en tout on peut créer c lignes. Là encore, le raisonnement est simple : chaque combinaison peut donner deux résultats en sortie, 0 et 1, le résultat de chaque combinaison est indépendant des autres, ce qui fait :
- .
Pour les portes logiques à 1 bit d’entrée, cela fait 4 portes logiques. Pour les portes logiques à 2 bits d’entrée, cela fait 16 portes logiques. Pour les portes logiques à 3 bits d’entrée, cela fait 256 portes logiques.
Les portes logiques à un bit d'entrée
[modifier | modifier le wikicode]Il existe quatre portes logiques de 1 bit. Il est facile de toutes les trouver avec un petit peu de réflexion, en testant tous les cas possibles.
- La première donne toujours un zéro en sortie, c'est la porte FALSE ;
- La seconde recopie l'entrée sur sa sortie, c'est la porte OUI, aussi appelée la porte BUFFER ;
- La troisième est la porte NON vue plus haut ;
- La première donne toujours un 1 en sortie, c'est la porte TRUE.
| Entrée | FALSE | OUI | NON | TRUE | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 1 |
On peut fabriquer une porte OUI en faisant suivre deux portes NON l'une à la suite de l'autre. Inverser un bit deux fois redonne le bit original.

Les portes logiques TRUE et FALSE sont des portes logiques un peu à part, qu'on appelle des portes triviales. Elles sont absolument inutiles et n'ont même pas de symbole attitré. Il est possible de fabriquer une porte FALSE à partir d'une porte TRUE suivie d'une porte NON, et inversement, de créer une porte TRUE en inversant la sortie d'une porte FALSE. Pour résumer, toutes les portes à une entrée peuvent se fabriquer en prenant une porte NON, couplée avec soit une porte FALSE, soit une porte TRUE. C'est étrange que l'on doive faire un choix arbitraire, mais c'est comme ça et la même chose arrivera quand on parlera des portes à deux entrées.
Les portes logiques à deux bits d'entrée
[modifier | modifier le wikicode]Les portes logiques à 2 bits d'entrée sont au nombre de 16. Et dans ces 16 portes, sont inclues les portes logiques à une entrée, à savoir les portes logiques FALSE, TRUE, OUI et NON. La porte OUI est en double, avec une porte qui recopie l'entrée A, une autre qui recopie l'entrée . De même, on trouve deux portes NON : une qui inverse l'entrée A et une autre qui inverse l'entrée B. En clair, sur les 16 portes logiques à deux entrées, 6 d'entre elles sont des portes à une entrée. Elles ont deux entrées, mais l'une d'entre elle n'est pas prise en compte. Seules 10 sont de vraies portes à deux entrées. Dans le tableau ci-dessous, avec les portes à une entrée illustrées en bleu.
| Entrée | FALSE | NOR | NCONVERSE | NON (A) | NIMPLY | NON (B) | XOR | NAND | ET | NXOR | OUI (B) | IMPLY | OUI (A) | CONVERSE | OU | TRUE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 01 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 10 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Les 10 portes logiques restantes peuvent se fabriquer en combinant d'autres portes logiques de base. Par exemple, certaines portes sont l'inverse l'une de l'autre. La porte ET et la porte NAND sont l'inverse l'une de l'autre : il suffit d'en combiner une avec une porte NON pour obtenir l'autre. Même chose pour les portes OU et NOR, ainsi que les portes XOR et NXOR. De fait, la moitié des portes logiques sont l'inverse de l'autre.
| Porte ET | 
|
|---|---|
| Porte OU | 
|
Mais dans ce qui suit, nous allons voir que certaines portes logiques sont des dérivées des portes ET et des portes OU, formées en combinant une porte ET/OU avec une ou plusieurs portes NON. Les portes logiques dérivées de la porte ET sont illustrées en rouge dans le tableau suivant, celles dérivées de la porte OU sont en vert, les portes XOR/NXOR sont en jaune, le reste est les portes à une entrée.
| Entrée | FALSE | NOR | NCONVERSE | NON A | NIMPLY | NON (B) | XOR | NAND | ET | NXOR | OUI (B) | IMPLY | OUI (A) | CONVERSE | OU | TRUE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 01 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 10 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Les portes dérivées de la porte OU
[modifier | modifier le wikicode]Les portes dérivées de la porte OU regroupent les deux portes OU et NAND, ainsi que deux nouvelles portes : IMPLY et CONVERSE. Elles sont équivalentes à une porte OU dont on aurait inversé une des entrées. Leurs symboles trahissent cet état de fait, jugez-en vous-même :
 |
 |
Vous vous demandez certainement ce qui se passe quand on inverse les deux entrées avant le OU. Un bon moyen de s'en rendre compte serait d'écrire la table de vérité de ce petit circuit, et le résultat que vous retomberez exactement sur la table de vérité d'une porte NAND. En clair, une porte NAND est équivalente à une porte OU dont on aurait inversé les deux entrées.

Les portes dérivées d'un OU mettent leur sortie à 1 pour trois lignes de la table de vérité, pour trois entrées possibles. Aussi, on les appellera des portes 3-combinaisons.
| Entrée | NAND | OR | CONVERSE | IMPLY |
|---|---|---|---|---|
| 00 | 1 | 0 | 1 | 1 |
| 01 | 1 | 1 | 0 | 1 |
| 10 | 1 | 1 | 1 | 0 |
| 11 | 0 | 1 | 1 | 1 |
Les portes dérivées de la porte ET
[modifier | modifier le wikicode]Les portes dérivées de la porte ET regroupent les deux portes NOR et ET, ainsi que deux nouvelles portes : NCONVERSE et NIMPLY, qui sont respectivement l'inverse des portes CONVERSE et IMPLY. Elles ont une sortie à 1 à condition que l'une des entrées soit à 1, et l'autre entrée soit à 0. On devine rapidement que ces deux portes peuvent se fabriquer en prenant une porte ET et en ajoutant une porte NON sur l'entrée adéquate. Au passage, cela se ressent dans les symboles utilisés pour ces deux portes, qui sont les suivants :
 |
 |
Vous vous demandez certainement ce qui se passe quand on inverse les deux entrées avant le ET. Encore une fois, il faut pour cela écrire la table de vérité du circuit. Et le résultat est la table de vérité d'une porte NOR. En clair, une porte NOR est équivalente à une porte ET dont on aurait inversé les deux entrées.

Les portes dérivées d'un ET mettent leur sortie à 1 pour une seule combinaison d'entrée, une seule ligne de la table de vérité. Aussi, nous allons les appeler des portes 1-combinaison.
| Entrée | NOR | NCONVERSE | NIMPLY | ET |
|---|---|---|---|---|
| 00 | 1 | 0 | 0 | 0 |
| 01 | 0 | 1 | 0 | 0 |
| 10 | 0 | 0 | 1 | 0 |
| 11 | 0 | 0 | 0 | 1 |
Les liens entre portes 1 et 3-combinaisons
[modifier | modifier le wikicode]Il y a un lien assez fort entre les ports dérivées de la porte ET et celles dérivées de la porte OU. Pour comprendre pourquoi, regardez le tableau suivant, qui liste les portes 1 et 3-combinaison en paires. On voit que chaque porte 1-combinaison est l'exact inverse d'une porte 3-combinaison ! La conséquence est que l'on peut créer n'importe quelle porte 3-combinaison à partie d'une porte 1-combinaison, et réciproquement.
| Entrée | NOR | OU | NCONVERSE | CONVERSE | IMPLY | NIMPLY | ET | NAND | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| 01 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | |||
| 10 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | |||
| 11 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
Par exemple, nous avions vu plus haut que la porte NOR est une porte dérivée d'une porte ET. On peut créer une porte OU en ajoutant une porte NON à une porte NOR basée sur un ET, ce qui donne le circuit ci-dessous. Ou encore, nous avions vu plus haut que la porte NAND est une porte dérivée d'une porte OU. On peut créer une porte ET en ajoutant une porte NON à une porte NAND basée sur un OU, ce qui donne le circuit ci-dessous.
 |
 |
Les portes XOR/NXOR sont "superflues"
[modifier | modifier le wikicode]Dans cette section, nous allons montrer que les portes XOR/NXOR peuvent se fabriquer à partir d'autres portes logiques. Il y a deux manières pour concevoir une porte XOR/NXOR à partir de portes ET/OU/NON. La première méthode combine plusieurs portes 1-combinaison avec une porte OU. L'autre méthode fait l'inverse : on combine plusieurs portes 3-combinaisons avec une porte ET.
La première méthode : combiner des portes dérivée d'un ET avec un OU
[modifier | modifier le wikicode]Commençons par le cas d'une porte XOR. La sortie d'une porte XOR est à 1 dans deux situations : soit la première entrée est à 1 et l'autre à 0, soit c'est l'inverse. Les deux cas correspondent respectivement aux portes NCONVERSE et NIMPLY, vue précédemment.
| Entrée 1 | Entrée 2 | NCONVERSE | NIMPLY | (NCONVERSE) OU (NIMPLY) = XOR | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | ||
| 1 | 1 | 0 | 0 | 0 |
La sortie des deux circuits est combinée avec une porte OU, car une seule des deux situations rencontrées met la sortie à 1. Le circuit obtenu est le suivant :

- Notons que ce circuit nous donne une idée pour créer une porte NXOR : il suffit de remplacer la porte OU finale par une porte NOR.
La porte NXOR peut se concevoir à parti du même raisonnement. La porte NXOR sort un 1 dans deux cas : soit quand ses deux entrées sont à 1, soit quand elles sont toutes deux à 0. La porte ET a sa sortie à 1 dans le premier cas, alors que la porte NOR (une OU suivie d'une NOT) a sa sortie à 1 dans le second cas.
| Entrée 1 | Entrée 2 | NOR | ET | NXOR | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 | ||
| 0 | 1 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | 1 |
Reste à combiner les deux portes avec une porte OU. Le circuit obtenu est le suivant :

- Notons que ce circuit nous donne une troisième possibilité pour créer une porte XOR : il suffit de remplacer la porte OU finale par une porte NOR.
Il s'agit là d'une technique qui marche au-delà des portes XOR, et qui marche pour toutes les portes logiques. L'idée est de lister toutes les lignes de la table de vérité où la porte sort un 1. Pour chaque ligne, on prend la porte 1-combinaison adéquate : celle qui sort un 1 pour cette ligne. On effectue ensuite un OU entre toutes les portes dérivées d'un ET. cette technique permet de fabriquer directement toutes les portes logiques à deux entrées, sauf la porte FALSE. C'est la seule qui ne puisse être fabriquée à partir de portes 1-combinaison seules et qui demande d'utiliser une porte NON pour. On peut donc, en théorie, fabriquer toutes les portes logiques à partir de seulement les portes ET, OU et NON.
La seconde méthode : combiner des portes dérivées d'un OU avec un ET
[modifier | modifier le wikicode]Une porte logique peut être conçue avec une méthode opposée à la précédente. Au lieu de procéder par addition, on procède par soustraction. Cette méthode demande de prendre des portes 3-combinaison et de les combiner avec une porte ET. Elle permet de fabriquer toutes les portes logiques, sauf la porte TRUE.
Par exemple, prenons la porte XOR. On part du principe qu'un XOR est un OU, sauf dans le cas où les deux entrées sont à 1, cas qui peut se détecter avec une porte ET. Sauf qu'on veut que la porte sorte un 0 quand les deux entrées sont à 1, alors qu'un ET fait l'inverse, ce qui indique qu'on doit plutôt utiliser une porte NAND. Voici ce que cela donne :
| Entrée 1 | Entrée 2 | OU | NAND | XOR | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | 1 | ||
| 1 | 0 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 0 | 0 |
On voit qu'en faisant un ET entre les sortie des portes OU et NAND, on obtient le résultat voulu.

- Notons que ce circuit nous donne une idée pour créer une porte NXOR : il suffit de remplacer la porte ET finale par une porte NAND.
Les portes NAND et NOR permettent de fabriquer toutes les autres portes
[modifier | modifier le wikicode]Dans la section précédente, nous avons vu que toutes les portes logiques peuvent être créés soit uniquement à partir de portes ET/NAND , soit uniquement à partir de portes OU/NOR. Cependant, supposons que je conserve les portes ET/NAND : dois-je conserver la porte ET ou la porte NAND ? Les deux solutions ne sont pas équivalentes, car l'une permet de se passer de porte NON et pas l'autre ! Pour comprendre pourquoi, nous allons essayer de créer toutes les portes à une entrée à partir de portes ET/OU/NAND/NOR.
Il est possible de créer une porte OUI en utilisant une porte ET ou encore une porte OU, comme illustré ci-dessous. La raison est que si on fait un ET/OU entre un bit et lui-même, on retrouve le bit initial. Il s'agit d'une propriété particulière de ces portes, sur laquelle nous reviendrons rapidement dans le chapitre sur les circuits combinatoires, et qui sera très utile vers la fin du chapitre. Par contre, impossible de créer une porte NON facilement.
 |
 |
Maintenant, que se passe-t-il si on utilise une porte NAND/NOR ? La réponse est simple : on obtient une porte NON ! Pour comprendre pourquoi, il faut imaginer que la porte NAND/NOR est composée d'une porte ET/OU suivie par une porte NON. Le bit d'entrée subit un ET/OU avec lui-même, avant d'être inversé. Le passage dans le ET/OU se comporte comme une porte OUI, alors que la porte NON l'inverse.
| Circuit équivalent avec des NAND | Circuit équivalent avec des NOR | |
|---|---|---|
| Porte NON | 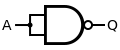 |
 |
- Vous vous demandez peut-être ce qu'il se passe quand on fait la même chose avec une porte XOR, en faisant un XOR entre un bit et lui-même. Et bien le résultat est une porte FALSE. En effet, la porte XOR fournit un zéro quand les deux bits d'entrée sont identiques, ce qui est le cas quand on XOR un bit avec lui-même. Et inversement, une porte TRUE peut se fabriquer en utilisant une porte NXOR. Il s'agit là d'une propriété particulière de la porte XOR/NXOR sur laquelle nous reviendrons rapidement dans le chapitre sur les circuits combinatoires, et qui sera très utile dans le chapitre sur les opérations bit à bit.
Créer les autres portes logiques est alors un jeu d'enfant avec ce qu'on a appris dans les sections précédentes. Il suffit de remplacer les portes NON et ET par leurs équivalents fabriqués avec des NAND.
On vient de voir qu'il est possible de fabriquer tout circuit avec seulement un type de porte logique : soit on construit le circuit avec uniquement des NAND, soit avec uniquement des NOR. Pour donner un exemple, sachez que les ordinateurs chargés du pilotage et de la navigation des missions Appollo étaient intégralement conçus avec des portes NOR.
Les portes logiques à plus de deux entrées
[modifier | modifier le wikicode]Par abus de langage, le terme "porte logique" désigne toutes les portes logiques à une ou deux entrées, mais pas au-delà. A l'exception de certains circuits assez simples, qui sont considérés comme des portes logiques même s'ils ont plus de deux entrées. En fait, une porte logique est un circuit simple, qui sert de brique de base pour d'autres circuits. En clair, les portes logiques sont des circuits élémentaires, et sont aux circuits électroniques ce que les atomes sont aux molécules. Dans ce qui suit, nous allons voir des portes logiques qui ont plus de 2 entrées. Beaucoup de ces circuits sont très utiles et reviendront régulièrement dans la suite du cours.
Les portes ET/OU/NAND/NOR à plusieurs entrées
[modifier | modifier le wikicode]Les premières portes logiques à plusieurs entrées que nous allons voir sont les portes ET/OU/NAND/NOR à plus de 2 entrées.
Il existe des portes ET qui ont plus de deux entrées. Elles peuvent en avoir 3, 4, 5, 6, 7, etc. Comme pour une porte ET normale, leur sortie ne vaut 1 que si toutes les entrées valent 1 : dans le cas contraire, la sortie de la porte ET vaut 0. Dit autrement, si une seule entrée vaut 0, la sortie de la porte ET vaut 0.
 |
 |
De même, il existe des portes OU/NOR à plus de deux entrées. Pour les portes OU à plusieurs entrées, leur sortie est à 1 quand au moins une de ses entrées vaut 1. Une autre manière de le dire est que leur sortie est à 0 si et seulement si toutes les entrées sont à 0.
 |
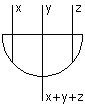 |
Les versions NAND et NOR existent elles aussiet leur sortie/comportement est l'inverse de celle d'une porte ET/OU à plusieurs entrées. Pour les portes NAND, leur sortie ne vaut 1 que si au moins une entrée est nulle : dans le cas contraire, la sortie de la porte NAND vaut 0. Dit autrement, si toutes les entrées sont à 1, la sortie vaut 0.
 |
 |
Bien sur, ces portes logiques peuvent se créer en combinant plusieurs portes ET/OU/NOR/NAND à deux entrées. Cependant, faire ainsi n'est pas la seule solution et nous verrons dans le chapitre suivant que l'on peut faire nettement mieux avec quelques transistors.
Elles sont très utiles dans la conception de circuits électroniques, mais elles sont aussi fortement utiles au niveau pédagogique. Nous en ferons un grand usage dans la suite du cours, car elles permettent de simplifier fortement les schémas et les explications pour certains circuits complexes. Sans elles, certains circuits seraient plus compliqués à comprendre, certains schémas seraient trop chargés en portes ET/OU pour être lisibles.
La porte à majorité
[modifier | modifier le wikicode]La porte à majorité est une porte à plusieurs entrées, qui met sa sortie à 1 quand une plus de la moitié des entrées sont à 1, et sort un 0 sinon. En général, le nombre d'entrée de cette porte est impair, pour éviter une situation où exactement la moitié des entrées sont à 1 et l'autre à 0. Il existe cependant des portes logiques à 4, 6, 8 entrées, mais elles sont plus rares.
Une porte à majorité est souvent fabriquée à partir de portes logiques simples (ET, OU, NON, NAND, NOR). Mais on considère que c'est une porte logique car c'est un circuit simple et utile. De plus, il est possible de créer une grande partie des circuits électroniques possibles en utilisant seulement des portes à majorité !
Voici le circuit d'une porte à majorité à trois entrées :

Voici le circuit d'une porte à majorité à 4 bits d'entrées :

Les deux circuits précédents nous disent comment fabriquer une porte à majorité générale. Pour la porte à trois entrée, on prend toutes les paires d'entrées possibles, on fait un ET entre les bits de chaque paire, puis on fait un OU entre le résultat des ET. Pareil pour la porte à 4 entrées : on prend toutes les combinaisons de trois entrées possibles, on fait un ET par combinaison, et on fait un OU entre tout le reste. Pour une porte à 5 entrées, on devrait utiliser là encore les combinaisons de trois entrées possibles. En fait, la recette générale est la suivante : pour une porte à N entrées, on toutes les combinaisons de (N+1)/2 entrées, on fait un ET par combinaison, puis on fait un OU entre les résultats des ET.
La porte à transmission
[modifier | modifier le wikicode]La porte à transmission est une porte logique assez particulière, qui mérite d'être vue dans ce chapitre. Pour simplifier, il s'agit d'un interrupteur commandable. Le circuit peut soit connecter l'entrée et la sortie, soit les déconnecter. Pour rappel, un interrupteur fermé laisse passer le courant, alors qu'un interrupteur fermé ne le laisse pas passer. Pour choisir entre les deux, une porte à transmission possède une entrée de commande sur laquelle on envoie un bit de commande, qui ouvre ou ferme l'interrupteur. La porte est typiquement fermée si le bit de commande est à 1, ouvert s'il est à 1.

Il est possible de la voir comme une porte OUI améliorée dont la table de vérité est celle-ci :
| Commande | Entrée | Sortie |
|---|---|---|
| 0 | 0 | Déconnexion |
| 0 | 1 | Déconnexion |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

Les portes à transmission sont très utilisés dans certains circuits très communs, que nous aborderons dans quelques chapitres, comme les multiplexeurs ou les démultiplexeurs.
Un défaut de ces portes logique est qu'elles sont électriquement équivalentes à des interrupteurs. Les autres portes logiques peuvent générer un 1 ou un 0 distinct de ce qu'il y a sur leur entrée. Et ce n'est pas un prodige, c'est juste que les portes logiques sont toutes reliées à la tension d'alimentation et à la masse (le 0 volt). Elles sont alimentées en électricité, pour fournir un 1 en sortie si l'entrée est à 0. Pas les portes à transmission, qui ne sont pas reliées à l'alimentation. Ce détail ne pose pas de problèmes tant qu'on n'enchaine pas de portes à transmission les unes à la suite des autres.